Hey everyone,
A few short updates:
Training
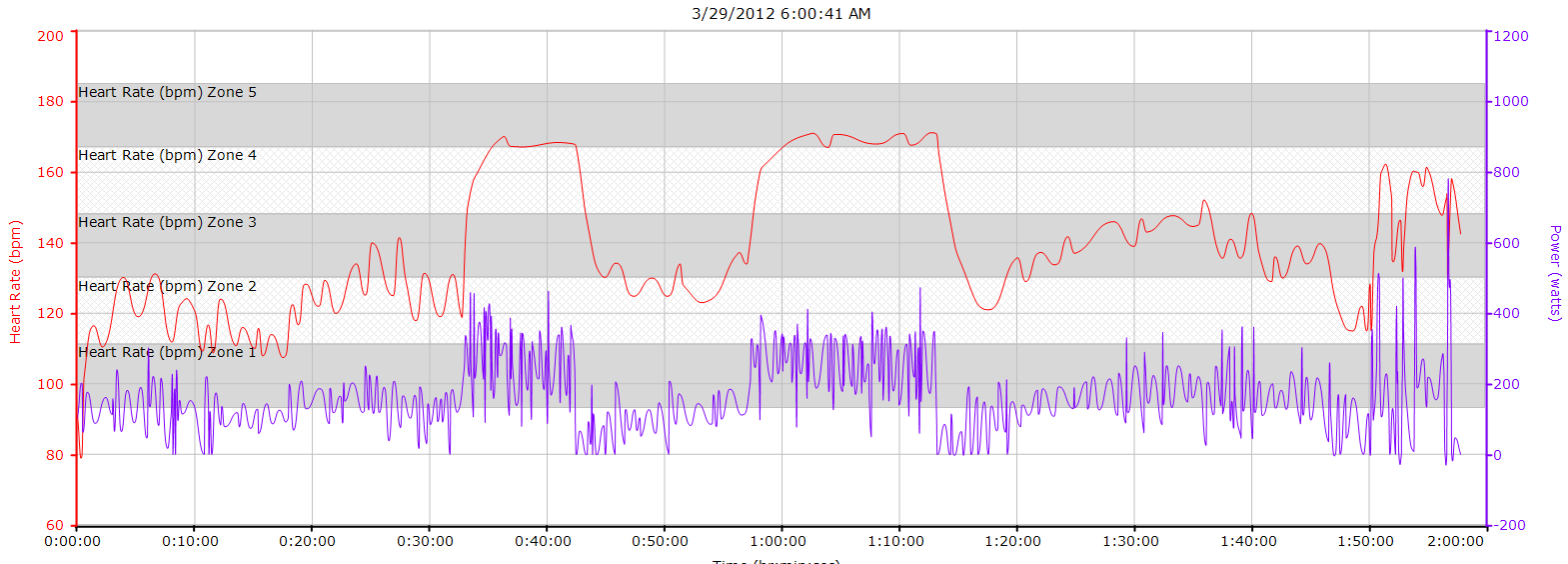
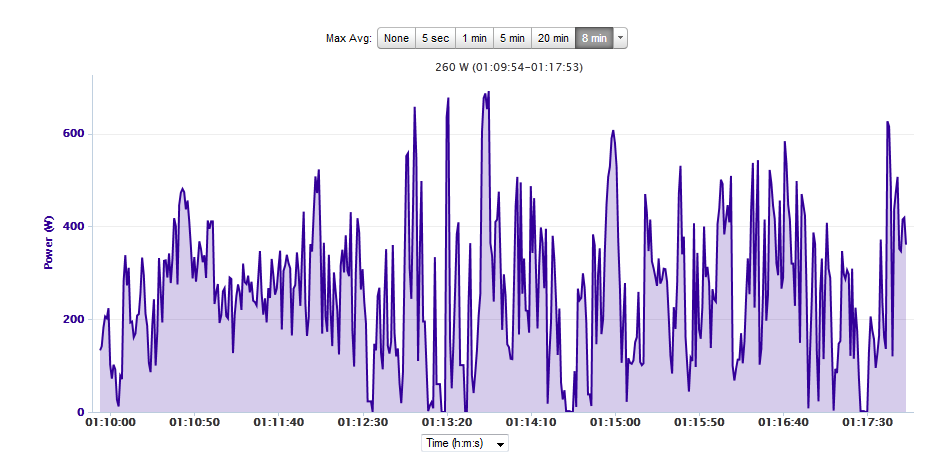
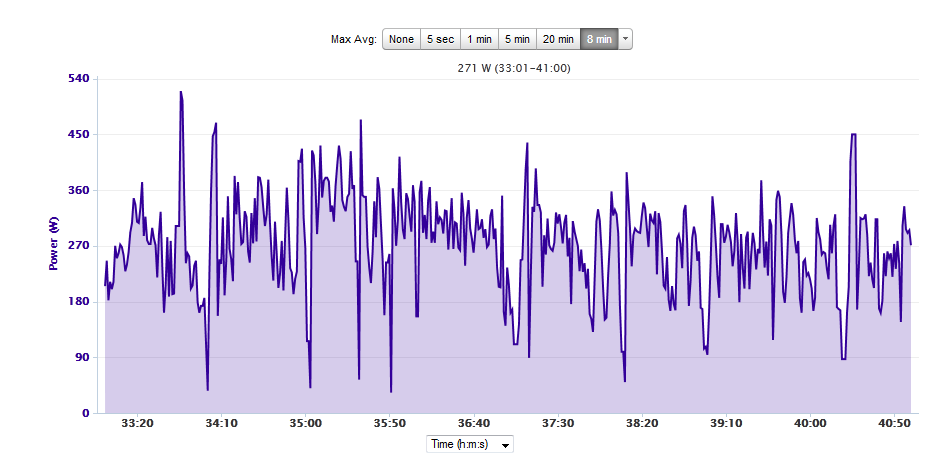
Last week I decided to take it easy, so on each of the training rides I deliberately kept my heart rate at or below 140 bpm. For weights, I deloaded my squats from 215 pounds to 140 pounds, which feels really light. I didn’t drastically cut back on the other exercises since I don’t have fatigue in my upper body. On Saturday, I met up with my friend Mark Knight from the Rice collegiate team, and we rode around the South Loop for about two hours, with him pulling the entire time at around 160 bpm. I was able to keep my HR at around 135 by drafting. I asked him how long he could sustain that heart rate, and in reply he told me “pretty much all day.” I can hold 160 for about 55 minutes (1×20 min & 1×25 min)…I think 1 consecutive hour is well within reach, so I’ll make that my next goal. In the meantime, I’ve decided to take it easy for another week. Then, I’ll start building with short 160 bpm efforts, gradually increasing the duration until I can sustain it for an hour.
Studying
I’ve picked up the pace of studying, but I still feel behind. The difficult thing about studying as an adult is that I don’t have the luxury of asking a professor for help, so I’m mostly doing it on my own. The notation can be intimidating at times, but the most important thing is to understand the purpose of the theory and how it applies to actuarial practice. For instance, last week I was reviewing Credibility Theory, which attempts to construct a flexible model for the pricing of insurance policies in a world where the underlying variables of risk constantly change. Charging too low of a price leaves the company vulnerable to heavy losses whereas charging too high of a price leaves the company vulnerable to competitors that charge more attractive rates. However, once you find the market rate, you have to develop a model that takes into consideration the fact that risks evolve over time. Credibility Theory allows us to compare the predictive power of a theoretical model against empirical data, which we’ve observed in the form of claims, losses, or payments. If the characteristics of the observed data differ substantially from those of the theoretical model, more weight is given to our prior experience than to the model itself.
Academic actuaries strive to create mathematical justification for current actuarial practices. The following example provides a glimpse of how actuaries link Credibility Theory to Bayesian Statistics. We can represent a sequence of independently distributed losses 1,…,n as a vector:
$latex displaystyle mbox{bfseries{X}} = (X_1,ldots,X_n)^T $
Where each Xj has the probability density function:
$latex displaystyle f_{X_j|Theta}(x_j), quad j = 1,ldots,n,n+1 $
The parameter Θ represents the unknown risk parameter, which allows for some level of uncertainty and heterogeneity amongst individual policyholders. The following equation represents the joint density function of the Xjs, given our risk parameter, Θ:
$latex displaystyle f_{mathbf{X},Theta}(mathbf{x},theta)=f(x_1,ldots,x_n| theta)left [prod^n_{j=1}f_{X_j|Theta}(x_j|theta)right]pi(theta)$
We can then integrate to obtain the marginal density function of x:
$latex displaystyle f_{mathbf{X}}(mathbf{x})=intleft[prod^n_{j=1}f_{X_j|Theta}(x_j|theta)right]pi(theta),mathrm{d}theta $
Where π(θ) represents the density function of our risk parameter Θ. We now want to predict our next loss, Xn_1, based on our past experience, X. We can now do so using the above formula to construct the conditional density of Xn_1, given X:
$latex displaystyle f_{X_{n+1}|mathbf{X}}(x_{n+1}|mathbf{x})=frac{1}{f_{mathbf{X}}(mathbf{x})}intleft[prod^{n+1}_{j=1}f_{X_j|Theta}(x_j|theta)right]pi(theta),mathrm{d}theta $
Using the definition of the posterior distribution from Bayesian Statistics, we define the posterior density function of Θ as:
$latex displaystyle pi_{Theta|mathbf{X}}(theta|mathbf{x})=frac{f_{mathbf{X},Theta}(mathbf{x},theta)}{f_mathbf{X}(mathbf{x})}=frac{1}{f_mathbf{X}(mathbf{x})}left[prod^n_{j=1}f_{X_j|Theta}(x_j|theta)right]pi(theta) $
Rearrangement of this definition yields:
$latex displaystyle left[prod^n_{j=1}f_{X_j|Theta}(x_j|theta)right]pi(theta)=pi_{Theta|mathbf{X}}(theta|mathbf{x})f_{mathbf{X}}(mathbf{x}) $
We can now substitute the right side of this equation into the numerator of the conditional density function of Xn_1, which yields:
$latex displaystyle f_{X_{n+1}|mathbf{X}}(x_{n+1}|mathbf{x})=int f_{X_{n+1}|Theta}(x_{n+1}|theta)pi_{Theta|mathbf{X}}(theta|mathbf{x}),mathrm{d}theta $
The conditional density function of Xn_1 now has the form of the density function of the predictive distribution from Bayesian Statistics. Thus, we have established (a small part of) Credibility Theory as a form of Bayesian Statistics.