Monthly Archives: January 2012

You are browsing the site archives by month.

No. 46: Project 3: An Arithmetic Trainer (Part 1)

31 January, 2012 3:55 AM / Leave a Comment /

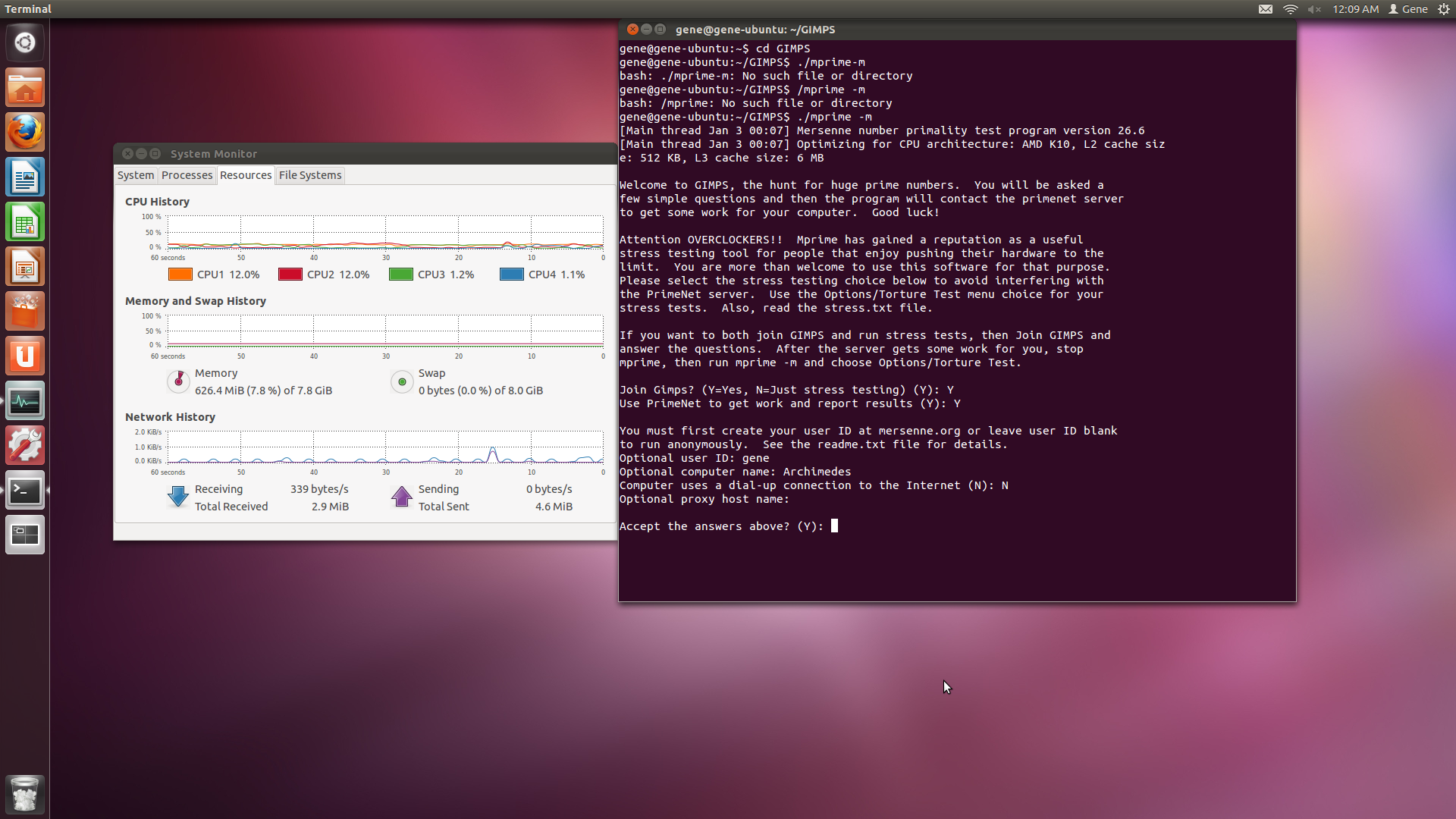
Hey everyone,

I mentioned last week that I began working on an arithmetic trainer for one of my side projects. I began programming a little more than a year ago and I wrote one of my first programs using Python, a simple multiplication tutor that tests the user on the multiplication of two-digit numbers. I’ve always wanted to to get good at arithmetic but somehow after I learned the times table in elementary school I stopped taking it seriously for various reasons, mainly because I was a kid and didn’t know any better. Anyway, the importance of arithmetic has waned over the years since the use of calculators has made mental computation a trivial task. However, I think dependence on technology makes kids overlook many of the creative methods our predecessors used to simplify tedious calculations. For example, legend has it that when Gauss was a schoolboy, his teacher told the class to find the sum of the integers from 1 to 100, just to assign them busywork while he was grading papers. However, instead of taking the direct approach and solving for $latex 1+2+cdots+100$ one term at a time, Gauss cleverly solved it using the following mental image:

Twice the sum of the first 100 integers.

First, write down the sum on one line, and then write it down again, except with the terms in the opposite order. You can see that the image above gives you 100 groups of 101, so you can multiply 100 by 101 to get 10,100. Since you’ve written down the sum of 1 to 100 twice, you have to divide by 2 to get the answer: 5,050. Isn’t that so much faster than adding them one at a time? Indeed, the general formula, $latex frac{n(n+1)}{2}$ gives you the sum of the first $latex n$ consecutive integers.

Unfortunately, I think the 1 through 10 arithmetic of the modern-day education system prevents our elementary students from discovering a lot of interesting patterns, especially when it comes to the squares of numbers, for example $latex 9*16 = 144 = 12^2=3^2*4^2=3^2*2^4$. There exist of course, countless patterns amongst the first 100 natural numbers. I’ve decided that the mastering of the basic arithmetic operations over the first 100 positive integers should give a young student a solid background and an ample set of numbers from which to identify patterns. However, it’s hard to train yourself without a pseudo random number generator giving you some variation, so, to facilitate the education of arithmetic, I decided to write a program in VBA to improve upon what I had done with my first Python program. I decided that the user needed more functionality – the user needs the ability to select the subset of numbers with which he/she decides to practice, as well as the operator to use in the calculations. Furthermore, the user needs to have the program monitor their performance over time. Thus, I developed my program through Microsoft Excel and you can see the basic interface here:

The basic interface.

In this example, I chose to have the program train me on all the multiples of 6 from 0-20. The program builds an array of factors, shuffles them into a random order, and prints them on the screen. You can see from the picture that I completed all the operations in about 13.83 seconds – a relatively good performance. I can do it much faster in my head but since I have to physically type the numbers I have to slow down somewhat. I like to read the numbers in groups of three and then simultaneously multiply these groups three at a time in my head before typing them out:

I do the operations three at a time.

The graph shows my progress over 52 attempts and you can see that I’ve improved over time. I programmed Excel to generate an embedded chart on the click of the button “Progress Chart.” The program fits a power curve to the data. I initially had the program fit a linear curve but I decided since most people should hit a wall at around the 11-12 second range, a power curve would better demonstrate the diminishing marginal returns of efficiency with each iteration.

I had Excel time the user during each attempt, and store the data once the user finished, given that they finished with 100% correct answers. The program prints the data into a database located on a hidden sheet:

The database is located on a hidden page

From here you can see that I’ve logged 415 attempts. The first column records the date of the trial, the second records the selected factors, the fourth records the operation, the fifth records the completion time, the sixth records the type of data (either all permutations of the selected factors or a limited subset). The program uses this database to create hidden pivot tables from which to generate charts. I got the program to display the chart embedded on a UserForm by saving the chart as a temporary file, uploading it onto a UserForm, and then deleting the temporary file. Unfortunately there’s a current bug where if you have a file called “chart.gif” anywhere in the workbook directory, Excel will override this file! I’ll change the coding to give the chart a more unique name, like”chartgd01″ or something like that. You normally don’t think of Excel as a teaching tool but it can definitely do much more than organize information. This is just one example.

You can try out the program by downloading it here. You need Excel 2007, and you need to enable macros to run this. You can find the instructions on the second sheet. The program is currently in prototype stage and is not finished yet. For example, the quotient operation is not yet functional. If you find any bugs, please tell me! On a side note, I’ve bridged the page deficit for my European History book and I’m now on track on page 835 out of about 1130. Right now I’m covering the nationalist movements following the Napoleonic wars.

Here’s the source code. I apologize for the lack of comments. I’ll include them for the next version. I’ve divided the program into two modules and one UserForm, along with an event handler that tells the program when the user has finished:

Module 1:

[code]Option Explicit
Sub mutli()

Dim factor As Integer, upper As Integer, lower As Integer, slower As Integer, supper As Integer, limitsize As Long
Dim x As Integer, y As Integer, z As Integer
Dim farray() As Variant, ansarray() As Variant, sarray() As Variant, printarray() As Variant, finalarray() As Variant, limitedarray As Variant
Dim prodcount As Long

factor = Range("FACTOR1L")
lower = Range("FACTOR2L")
upper = Range("FACTOR2U")
slower = Range("FACTOR1L")
supper = Range("FACTOR1U")
limitsize = Range("SIZE")

Sheets("Trial").Select
Range("A2:D1048576").Clear
Range("STATUS").Value = False

ReDim farray(lower To upper) As Variant
ReDim sarray(slower To supper) As Variant
ReDim limitedarray(1 To Range("SIZE"), 1 To 2)

For x = lower To upper
farray(x) = x
Next x

For y = slower To supper
sarray(y) = y
Next y

prodcount = WorksheetFunction.Count(farray) * WorksheetFunction.Count(sarray)

If Range("LIMITEDSAMPLE") = True And (Range("SIZE") > prodcount) Then
MsgBox "Error: sample size is larger than the possible number of permutations. Select a smaller sample or set ""Limited Sample"" to ""FALSE""."
Debug.Print "hithere"
Exit Sub
End If

ReDim finalarray(1 To prodcount) As Variant

z = 1
For x = slower To supper
For y = lower To upper
finalarray(z) = x & ":" & y
z = z + 1
Next y
Next x

finalarray() = ShuffleArray(finalarray)

ReDim printarray(1 To prodcount, 1 To 2)
For x = 1 To prodcount
printarray(x, 1) = Left(finalarray(x), WorksheetFunction.Search(":", finalarray(x)) – 1)
printarray(x, 2) = Right(finalarray(x), Len(finalarray(x)) – WorksheetFunction.Search(":", finalarray(x)))
Next x

If Range("LIMITEDSAMPLE") = True Then
For x = 1 To Range("SIZE")
limitedarray(x, 1) = printarray(x, 1)
limitedarray(x, 2) = printarray(x, 2)
Next x
End If

If Range("LIMITEDSAMPLE") = True Then
Range("A2:B" & Range("SIZE") + 1).Value = limitedarray
Application.Names.Add Name:="END", RefersTo:=Range("C" & limitsize + 2)
Application.Names.Add Name:="PRODUCTCOUNT", RefersTo:=limitsize
ElseIf Range("LimitedSample") = False Then
Range("A2:B" & prodcount + 1).Value = printarray
Application.Names.Add Name:="END", RefersTo:=Range("C" & prodcount + 2)
Application.Names.Add Name:="PRODUCTCOUNT", RefersTo:=prodcount
End If

Range("C" & WorksheetFunction.Count(Range("A:A")) + 2).Value = "END"
Range("ANSWER").Select

Range("FTIME") = Timer
Range("FTIME").Font.Color = RGB(255, 255, 255)

End Sub

Function ShuffleArray(InArray() As Variant) As Variant()
””””””””””””””””””””””””””””””””””””””””””
‘ ShuffleArray
‘ This function returns the values of InArray in random order. The original
‘ InArray is not modified.
””””””””””””””””””””””””””””””””””””””””””
Dim N As Long
Dim L As Long
Dim Temp As Variant
Dim J As Long
Dim Arr() As Variant

Randomize
L = UBound(InArray) – LBound(InArray) + 1
ReDim Arr(LBound(InArray) To UBound(InArray))
For N = LBound(InArray) To UBound(InArray)
Arr(N) = InArray(N)
Next N
For N = LBound(InArray) To UBound(InArray)
J = Int((UBound(InArray) – LBound(InArray) + 1) * Rnd + LBound(InArray))
If N <> J Then
Temp = Arr(N)
Arr(N) = Arr(J)
Arr(J) = Temp
End If
Next N
ShuffleArray = Arr
End Function

Sub check()

Dim x As Integer, y As Integer, z As Integer, currentrow As Long
Dim resultsinfo() As Variant
Dim finishtime As Single
Dim checkcount As Variant

Application.ScreenUpdating = False

finishtime = Timer – Range("FTIME")
checkcount = Right(Names("PRODUCTCOUNT").Value, Len(Names("PRODUCTCOUNT")) – 1)

ReDim resultsinfo(1 To 6) As Variant
y = 0

If Range("Operator").Value = "Product" Then
For x = 1 To checkcount
If Range("A" & x + 1) * Range("B" & x + 1) = Range("C" & x + 1) Then
Range("D" & x + 1).Value = "TRUE"
y = y + 1
Else
Range("D" & x + 1).Value = "FALSE"
End If
Next x

ElseIf Range("Operator").Value = "Sum" Then
For x = 1 To checkcount
If Range("A" & x + 1) + Range("B" & x + 1) = Range("C" & x + 1) Then
Range("D" & x + 1).Value = "TRUE"
y = y + 1
Else
Range("D" & x + 1).Value = "FALSE"
End If
Next x

ElseIf Range("Operator").Value = "Difference" Then
For x = 1 To checkcount
If Range("A" & x + 1) – Range("B" & x + 1) = Range("C" & x + 1) Then
Range("D" & x + 1).Value = "TRUE"
y = y + 1
Else
Range("D" & x + 2).Value = "FALSE"
End If
Next x
End If

Range("GRADE") = y / (checkcount)
resultsinfo(1) = Now
resultsinfo(2) = Range("FACTOR1L").Value & ":" & Range("factor1u").Value & "-" & Range("Factor2L").Value & ":" & Range("Factor2U").Value
resultsinfo(3) = Range("OPERATOR").Value
resultsinfo(4) = finishtime
If Range("LIMITEDSAMPLE") = True Then
resultsinfo(5) = "Limited"
ElseIf Range("LIMITEDSAMPLE") = False Then
resultsinfo(5) = "Full"
End If
resultsinfo(6) = checkcount

currentrow = WorksheetFunction.CountA(Sheets("Database").Range("A:A")) + 1

If (Range("GRADE") = 1 And Range("STATUS") = False) Then
Range("STATUS").Value = True
For z = 1 To 6
Range("FTIME") = finishtime
Sheets("Database").Range(Chr(64 + z) & currentrow).Value = resultsinfo(z)
Next z
ElseIf Range("STATUS") = False Then
Range("FTIME") = finishtime
Range("STATUS").Value = True
End If

Range("FTIME").Font.Color = RGB(0, 0, 0)

createpivot

Application.ScreenUpdating = True
End Sub

Sub createpivot()

Dim resultscache As PivotCache
Dim resultstable As PivotTable
Dim factorpt As PivotTable

Sheets("Pivot").UsedRange.Clear
Sheets("FormPivot").UsedRange.Clear

Set resultscache = ActiveWorkbook.PivotCaches.Create(SourceType:=xlDatabase, SourceData:=Sheets("Database").UsedRange)

Set resultstable = Sheets("Pivot").PivotTables.Add(PivotCache:=resultscache, TableDestination:=Sheets("Pivot").Range("A1"))
Set resultscache = ActiveWorkbook.PivotCaches.Create(SourceType:=xlDatabase, SourceData:=Sheets("Database").UsedRange)
Set factorpt = Sheets("FormPivot").PivotTables.Add(PivotCache:=resultscache, TableDestination:=Sheets("FormPivot").Range("A1"))

With resultstable
.PivotFields("CompletionTime").Orientation = xlDataField
.PivotFields("Date").Orientation = xlRowField
.PivotFields("Operation").Orientation = xlPageField
.PivotFields("Factors").Orientation = xlPageField
End With

With factorpt
.PivotFields("Factors").Orientation = xlRowField
End With

End Sub

[/code]

Module 2:

[code]
Option Explicit

Sub showchart()
UserForm1.Show
End Sub
[/code]

UserForm1:

[code]

Option Explicit

Private Sub ComboBox2_Change()
End Sub

Private Sub CommandButton1_Click()

Dim chartrange As Range
Dim progresschart As Chart
Dim factors As String
Dim factoritem As Variant
Dim inlist As Boolean
Dim chartcount As Long

inlist = False
factors = UserForm1.selectedfactor

For Each factoritem In UserForm1.selectedfactor.List
If factors = factoritem Then
inlist = True
End If
Next factoritem

If inlist = False Then
MsgBox prompt:="Invalid selection", Buttons:=vbExclamation
Exit Sub
End If

With Sheets("Pivot").PivotTables(1)
.PivotFields("Operation").CurrentPage = UserForm1.selectedoperator.Value
.PivotFields("Factors").CurrentPage = UserForm1.selectedfactor.Value
End With

Set chartrange = Sheets("Pivot").Range("A5:B" & WorksheetFunction.Count(Sheets("Pivot").Range("B:B")) + 3)

Set progresschart = Sheets("Pivot").Shapes.AddChart.Chart
With progresschart
.SetSourceData Source:=chartrange
.ChartType = xlLine
.ChartTitle.Text = "Trial v.s. Completion Time – " & factors
.SeriesCollection(1).Trendlines.Add
.SeriesCollection(1).Trendlines(1).Type = xlPower
.ShowAllFieldButtons = False
.SetElement (msoElementLegendNone)
With .Axes(xlValue)
.HasTitle = True
.AxisTitle.Text = "Completion Time (Seconds)"
End With
With .Axes(xlCategory)
.HasTitle = True
.AxisTitle.Text = "Trial"
End With
End With

With Sheets("Pivot").ChartObjects(1)
.Width = 485
.Height = 330
End With

Sheets("Pivot").ChartObjects(1).Chart.Export Filename:=ThisWorkbook.Path & "chart.gif", filtername:="GIF"
UserForm1.Image1.Picture = LoadPicture(ThisWorkbook.Path & "chart.gif")

For chartcount = 1 To Sheets("pivot").ChartObjects.Count
Sheets("Pivot").ChartObjects(chartcount).Delete
Next chartcount

Kill (ThisWorkbook.Path & "chart.gif")

End Sub

Private Sub userform_activate()

Dim x As Long
Dim inlist As Boolean

inlist = False

With Me
.Left = Application.Left + Application.Width / 2 – .Width / 2
With selectedoperator
.AddItem ("Difference")
.AddItem ("Product")
.AddItem ("Sum")
.AddItem ("Quotient")
End With
.selectedoperator.Value = Range("OPERATOR").Value
.selectedfactor.Value = Range("FACTOR1L").Value & ":" & Range("FACTOR1U").Value & "-" & Range("Factor2L").Value & ":" & Range("Factor2U").Value
End With

For x = 2 To WorksheetFunction.CountA(Sheets("FormPivot").Range("A:A")) – 1
selectedfactor.AddItem (Sheets("FormPivot").Range("A" & x))
If selectedfactor.Value = Sheets("FormPivot").Range("A" & x) Then
inlist = True
End If
Next x

createpivot
If inlist = True Then
CommandButton1_Click
End If
End Sub

[/code]

Event Handler:

[code]

Private Sub TextBox1_Change()

End Sub

Private Sub Worksheet_SelectionChange(ByVal Target As Range)

Dim lower, upper As Integer

If Not Intersect(Target, Range("END")) Is Nothing Then
check
End If

End Sub[/code]

Posted in: Logs, Mathematics

No 45: A Few Updates

24 January, 2012 4:12 AM / Leave a Comment /

Hey everyone,

I have a few updates.

I fell on Saturday

Each Saturday, I drive back down to Clear Lake to ride my bike with the Space City Cycling Club for about 3 hours – about 60 miles. I had mistakenly checked the weather forecast for my own zip code which indicated clear skies but when I arrived in Clear Lake I encountered some mild precipitation. I had the appropriate clothing with me and the rain almost never poses a problem except for thunderstorms as I’ve ridden in the rain dozens of times over the last three years. Unfortunately, about 35 miles into the ride on the way back to Bike Barn, the group approached a series of railroad tracks and I fell while crossing the second set, which lie at roughly a 70 degree angle which makes it difficult for cyclists to cross them perpendicularly – the safest trajectory. The rain causes the oil deposits to rise to the surface, and the combination of oil and slick iron makes for a very slippery crossing. So, I fell over to the right and landed on the side of my torso, which I think is the safest way to land when you fall to the side. What you don’t want to do is stick your arm out to break the fall because that’s an easy way to break your arm or collarbone. Anyway, I didn’t have time to think about what to do as I only realized I had fallen after I had fallen. I slid out a few feet due to the rain which is nice because it mitigates the impact and the scrapes, although I did get a few since my elbow and hip made contact with the pavement. The people in the group were so nice and it was really considerate of them to stop and make sure I was okay. They helped me straighten out my shifters and I was back on the bike after a couple of minutes. Thankfully, I escaped with no broken bones and I really think the weightlifting’s paid off over the last few years in strengthening my muscles and bones, especially the power cleans which I started at the end of last year.

I listened to Rachmaninoff at Jones Hall

After I got home, I read a little bit of European history (as of today I’ve cut the deficit from 50 pages to 25 pages) and ate dinner before I went to see Kirill Gerstein play Rachmaninoff’s Piano Concerto No.2 with one of my friends whom I met at state orchestra back in high school, along with some of her friends from Rice. I don’t actually go to see concerts very often and during most of my young life I had been performing them more than listening to them. I really miss playing and if I didn’t hurt my hands I think I would still be practicing 3-4 hours a day, but I decided against surgery a couple years back because the doctor told me that there was a high chance of recurrence and that it wasn’t worth it unless I couldn’t do basic things like hold a spoon or button my shirt. However, I’m fine with not playing anymore and right now I think cycling, math, computers, and studying makes me about has happy as I was when I still played, though relatively I’m not as good at cycling and math as I was at playing – mainly because I haven’t pursued these interests for as long, but I’m sure I’ll reap the benefits over time. Anyway Kirill Gerstein put on a flawless performance and I really enjoyed the concert.

On stuyding

I completed writing down all the theorems I needed to know for exam C/4 – 107 in all, and you can download the pdf from my SkyDrive (file – “temp_mem_bank”). I plan to memorize all the theorems to work on my memory, even though I don’t have to strictly memorize them for the test. I also started a couple of other projects – using a random number generator for studying these theorems, which I mentioned last week, and also another tool for the study of arithmetic. These are still in the early stages so I didn’t include them here, but I’ll talk about them next week. Anyway, I really rushed though this post and even though I say that I’m really short on time for these posts I think that this was especially true this time as I’ve only had about half an hour to write this. The quality of the post is low, has way too many verbs to be, and it doesn’t reflect my best writing. What really took me back today was a stumbling block I ran into while doing some algebra problems – I had trouble finding complex solutions to cubic equations of the following form:

$latex displaystyle ax^3+bx^2+cx+d=0$

For example, I needed to solve for $latex x^3=-1$. I got the first root, -1, but I had trouble finding the complex roots which happened to be $latex frac{1}{2}pmfrac{sqrt{3}}{2}i$. Larson’s book briefly went over complex numbers and I did plenty of exercises that involved quadratic equations with imaginary parts to the solutions, but none involving cubic equations. I looked up how to solve for cubic roots on Wikipedia and the general solutions consist of some unpleasantly gargantuan equations:

General Solutions to Cubic Equations

I think the proof of this is beyond the book and I couldn’t even find these equations anywhere within the text. I shouldn’t have any trouble understanding the proof but I think as far as basic College Algebra goes I can just use the general solution until I move into discrete math, and then abstract algebra. Anyway, looking for how to solve the problems and then solving them set me back a couple hours, but it was worth it skimping out on the quality of this post to get the solutions. Anyway, I’m glad I found the equations and that I managed to complete this post on time.

Posted in: Logs

No. 44: A Brief Note on Studying

17 January, 2012 4:34 AM / 2 Comments /

On Studying

When I began the actuarial exam process a few years ago, I stumbled upon a personal essay from the SOA archives about Andrew Lin, a brilliant student who became full fellow at the age of 20. Even today, we actuaries and actuarial students consider this an extremely rare feat and an extraordinary display of intelligence. The most talented actuaries tend to achieve fellowship at the age of 25, about three years after college,  so I’d imagine that you could count the number of 24-or-younger FSAs on your left hand. Anyway, when reading the article you shouldn’t focus on how Lin achieved the designation so early – but more on how he, as a non-native speaker of English, motivated himself to learn 25 words of English each night for 9 consecutive months. 25 words doesn’t sound like a lot and you can’t hold an intelligent conversation with such a limited vocabulary. However, over the span of 9 months Lin would learn approximately 6,750 words. Had he continued the ritual for another two years he would have learned over 20,000 words – the size of the average vocabulary of a native English speaker. In addition to vocabulary, he devoted each night to learning non-school related material that he found interesting.

I’d say the article has left a lasting influence on the way I learn. Ever since I started my job in March, I decided, time permitting, to devote each night to reading something I found interesting at a rate of 100 pages per week. I started with the book A Mathematician’s Apology by G.H. Hardy and then moved on to Hackers by Steven Levy and shortly afterward to Atlas Shrugged by Ayn Rand. I got to the point where Dagny Taggart started having an affair with Hank Rearden but I later saw the book as dull and intellectually unstimulating (sorry, Ayn Rand fans) so I switched over to Norman Davies’ Europe, A History since I never took European History in high school. I figured that, in a manner similar to that of the preceding paragraph, if I read 100 pages a week I would have read over 5,000 pages after a year. Since I like to read textbooks (I have a Sociology book lined up after Davies), and each textbook is roughly about 1,000 pages, I concluded that I could read a college semester’s worth (or maybe even a year’s worth since college courses rarely cover the entire book) of material each year. This, in addition to the Actuarial curriculum and the projects I learn at work, makes for a very education-heavy lifestyle that I’ve come to enjoy.

I like to alternate between “Heavy” material and “Light” material as I complete each book. “Heavy” material consists of textbooks or academic material whereas “Light” material consists of pleasure reading, like novels. In an effort to speed up my reading (I don’t plan on doing only 100 pages a week forever), after I finish a “heavy” book, reading slowly to absorb the material, I start reading a “light” book and read it as fast as possible. For instance, I consider Davies as heavy material. The next book (a light book), Kingpin, tells the true story of Max Butler, aka “Iceman,” a computer criminal who stole 2 million credit cards and sold them on the black market. Another former criminal, Kevin Poulsen, now a journalist, wrote the book so I think this will present a unique perspective into the cybercriminal underworld. The book consists of about 250 pages, which I plan on reading over the span of a week (so about 2.5 times the speed of heavy material). The easily digestible nature of light material makes it an ideal source for developing my reading speed. After finishing Kingpin, I plan on going back to “Heavy” material, in this case – Sociology by John Macionis (since I never took a sociology course), except at a rate of 105 pages per week. The cycle continues in this manner until I can no longer read the required pages within the allotted amount of time, the point at which I reduce 10%-20% of the required page count and start the cycle again.  Unfortunately, this week marks the first time in 6 weeks that I’ve fallen behind schedule – by about 50 pages. I’ll let you know next week if I’ve caught up.

In addition to all this, I still have my actuarial material to study, along with the math/computer projects I do on the side when I’m not studying for exams. I’m still in the early stage of exam preparation and most of it consists of the rote memory of basic theorems and definitions that serve as the foundation of model construction. I felt inspired by Tesla’s ability to memorize complete books and for a while I wrote down some theorems (see “temp_mem_bank”) in $latex LaTeX$ using my RStudio server and tried using a random number generator to generate a theorem or definition number (say, Definition 2.5 from Klugman) and then trying to write down that theorem or definition verbatim, including the punctuation marks. Right now I’ve done this at a rate of 3 theorems a day but I find it really taxing. I feel a slight improvement in my memory but if I find that I haven’t gone anywhere after a month I might have to ditch this method for practical reasons to devote more time to solving problems.

As a side note, my tubulars arrived last week and I rode them last Saturday for a 3 hour training session back in Clear Lake. They feel fantastic. I had them up to 120 psi but it felt like I was riding at the comfort of 90 psi on clinchers. The wheels were extremely fast. They look pretty sweet too.

Cronus Ultimate with HED Stinger 6 Tubulars

Posted in: Logs

No. 43: A Perfect Score, Imperfect Preparation

10 January, 2012 2:19 AM / 1 Comment /

Hey everyone,

I just wanted to make this quick because I need to wake up early tomorrow. I just wanted to let you know that I received a perfect score of 10 on Exam MLC/3L, which I received today to my relief. This is my second perfect score – I got also got a 10 on FM/2 last year. I felt confident that I would pass but today confirmed how well I thought I did after I took the test. A score of 10 doesn’t mean that I answered every single question correctly, which I probably didn’t since I had to guess on a handful of them when I ran out of time towards the end of the test. Rather, the SOA determines an initial pass mark (usually around 18 or 19 of the 30 questions), equates that to a 6, and increments the score equating each previous or subsequent point to 10% of the pass mark. For instance, if they set the pass mark at 19, a score of 6 means you got 19 right on the exam. A score of 7 means you got 21 or 22 right (since 19 + 1.9 = 20.9), a score of 8 means you got 23 or 24 right, and so on.

A score of 10 means I finished somewhere on the right side of the distribution – but since the SOA doesn’t release the distribution of scores I can’t determine my percentile or performance relative to my peers, though they do release the pass rate which usually ends up somewhere between 40%-55% of the candidates. Although I do feel satisfied with the result, I don’t feel happy with the way I studied or prepared for the exam. I skipped the May sitting because I moved to Memorial for my new job, and I had to take care of a lot of “firsts” in life such as apartment rent, savings and retirement accounts, bills, and so on and so forth, which may or may not belong to the set of acceptable excuses for skipping an important professional exam. Furthermore, the SOA introduced significant changes to the MLC syllabus effective in 2012, so skipping the first sitting in 2011 meant that I only had one shot to pass before the exam change. Also, I only started studying in mid-August which gave me about 2.75 months to study (which may seem ideal for others, but short for me). I studied frantically, and I don’t think I paced myself well at all.

Anyway, I can at least put away the anxiety of the hardest preliminary exam, but I’ve made it my goal to not make the same mistakes as I have in the past. The next exam, C/4, from what I hear has easier problems than those in MLC, but the calculations require more steps, which leaves more space for human error so I have to tread carefully. The exam feels more like an older sibling to the first exam, P/1 since you work with probability distributions, but work with more sophisticated modeling techniques and more complicated distributions. I decided to change my method of study to include a lot more rote memory since the exam focuses more on knowledge of methods, rather than insight and creativity (the C/4 questions are more similar to “do this method on this data set” as opposed to the “what can you conclude from this” style questions found on MLC). I’ve already created a Temporary Memory Bank in written form (you can find the file on my sky drive as “temp_mem_bank”), which includes concepts that I’ve committed to memory for this test, but have not, as of now committed to permanent memory as I have in the Permanent Memory Bank.

I’ve set the word count limit for my posts as 500 for the minimum and 1000 for the maximum. I figured, that updating the blog with extremely short posts would not satisfy the requirements of a New Year’s resolution, so I decided that 500 words seemed appropriate since I had to write brief, 500-word essays every week during my English course of my first semester of college (in addition to 3 longer papers ~5 pages and a term paper ~20 pages). This post, at ~750 words, took me less than an hour. I put a limit of 1000 words since these are blog posts, not dissertations, and I feel no need to bore the time-conscious reader.

As a side note – I ordered some new tubulars for the 2012 race season. One of these is mine:

My new set of wheels is in there, somewhere. Photo by Philip Shama

Posted in: Logs / Tagged: , , , , ,

No. 42: The Great Internet Mersenne Prime Search – How to Install and Start GIMPS on Ubuntu 11.10

3 January, 2012 6:28 AM / 2 Comments /

Hey everyone,

When I said that I’d update this blog once a week, I didn’t realize that I’d have to post five times as many updates as I did last year. Fortunately, I don’t see this as something I can’t do so I decided to make it my new year’s resolution. Today I’ve decided to write about the Great Internet Mersenne Prime Search (GIMPS)- an online distributed computing project that aims to find Mersenne Primes.  Distributed computing means that several computers on a network work together on a certain task. In the case of the Great Mersenne Prime Search, these computers come from university computer labs, homes, and even video game consoles all across the world. Other distributed computing projects involve protein folding (perhaps the most famous), finding extraterrestrial life, searching for gravitational waves, and so on and so forth. These projects work by utilizing spare processing power from participating computers. All this processing power put together makes for a very powerful network, and these projects have already made important discoveries, such as a protein structure related to HIV. Anyway, after I set up my Linux server, which runs throughout the day, I decided that letting it run idly would waste a lot of processing power, so I decided to install a program from a distributed computing project. I chose GIMPS because I spent some time studying the Mersenne primes in school, so as a math major this project would come naturally to me. I couldn’t find a suitable setup guide for Ubuntu 11.10, however, so I decided to write one here.

About Mersenne Primes

We call numbers of the form $latex M_p = 2^p-1$ Mersenne Numbers. However, only a few of these Mersenne Numbers belong to the set of prime numbers, and as of 2009 we know of only 47 Mersenne Primes. The nature of Mersenne Primes makes them some of the largest known prime numbers out there, and indeed, the largest known prime, $latex 2^{43112609}-1$, is a Mersenne Prime. The Great Internet Mersenne Prime Search aims to find additional Mersenne Primes through distributed computing using the Lucas-Lehmer test for Mersenne Primes.

Downloading GIMPS

Go to the GIMPS homepage, and click on the link “Getting Started.” Go to the link called “Register a new user account login” and create your user account. After you create your account, go to the Download Software page and select the package appropriate for your operating system. Since I use 64-bit Ubuntu, I downloaded the 64-bit Linux package. Place the package into the desired directory. For my computer, I created a folder called “GIMPS” in my home folder, and put the package there.

Placing the package into the GIMPS folder and opening it with Archive Manager

Next, click open the package with Archive Manager and then extract the files. Archive Manager will extract the files into the GIMPS folder.

GIMPS folder after extraction

Next, open up the terminal (CTRL+ALT+T) and change the directory to the GIMPS folder (do this simply by typing “cd GIMPS”). Now, open the mprime folder by typing in the command “./mprime -m”. Remember the space! The program “mprime” is the main program that will do the primality testing.

Use these commands to start mprime

mprime will now ask you if you want to join GIMPS. Select yes. Then, mprime will ask you to create an optional user ID and computer name. Fill these out – for example I entered my name as “gene” and my computer name as “Archimedes.” You can leave the proxy host name blank, just press enter. Then, type “Y” when mprime asks you to accept the above answers.

Initial running of mprime

mprime will then ask you the number of hours per day the program will run, how much memory to let it use, and the number of workers (number of CPUs) that will run. The default answers to these questions are in parentheses (). I selected the defaults for all of them. You do have the option to use more memory to speed up the program, however. mprime will then ask you to set the work priorities for your computer. Go ahead and select all the defaults, this will allow mprime to automatically allocate work to your processors. After accepting the answers, you will see your terminal window fill up with a bunch of text. This text describes which Mersenne Numbers your CPUs are testing, how much progress they’ve made, and the estimated completion dates. Depending on how you set it up, you may have missed the main menu. On my first install I saw the menu right away, but on the second install the program seemed to have skipped over the menu.

Here is a screenshot of the menu:

mprime options menu

Go ahead and select option 3. This will give you a summary of the progress.

mprime at work, showing progress

You can see here that my version of mprime is currently testing Mersenne numbers M55085531, M55091137, M55093139, and M55093327 using the Lucas-Lehmer test. The number after the M is the p in $latex M_p = 2^p-1$. So as you can see, these are very large numbers. The odds of me finding a Mersenne prime are 1 in 113533 for this current batch of tests!

And that’s it! Press any key to continue, and select option 5 to exit.

Things to do

You can see from the last picture that mprime will cause your computer to constantly use 100% of its processing power, 24 hours a day. This somewhat concerns me when it comes to temperatures, as I don’t want things to overheat while I’m away from the computer or at work. So, I plan on writing a script to have the server save the temperature readings into a text file so I can check on it periodically from a phone or another computer, and in the case of an emergency I can shut it down remotely.

If you think there’s anything missing in this guide, or if you think you have anything useful to add, or if you find any errors, let me know! I’m always open to input from others.

Posted in: Logs, Mathematics / Tagged: , , , ,