Reading: Section 1.8 – Linear Transformations (On Target)
Problems: Section 1.6 – Applications of Linear Systems (Behind – 2 Days)
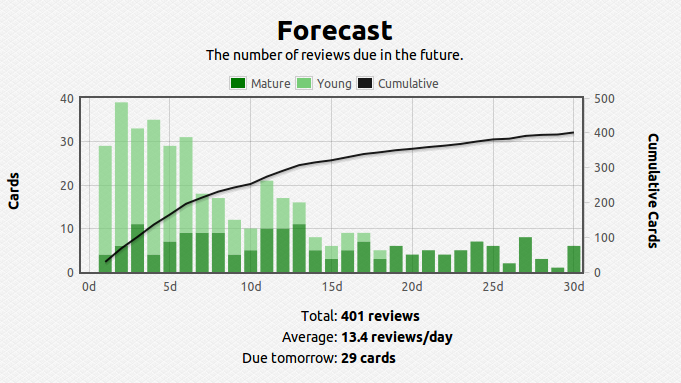
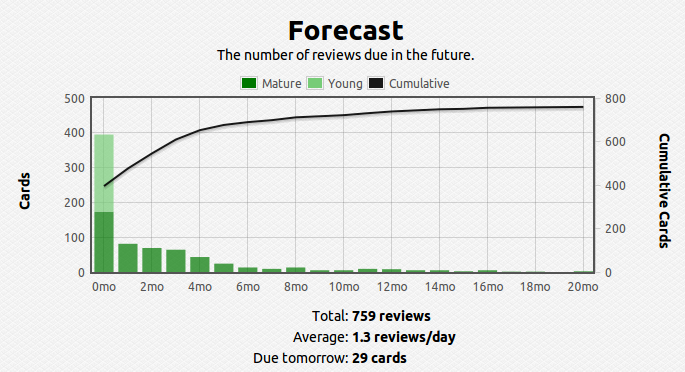
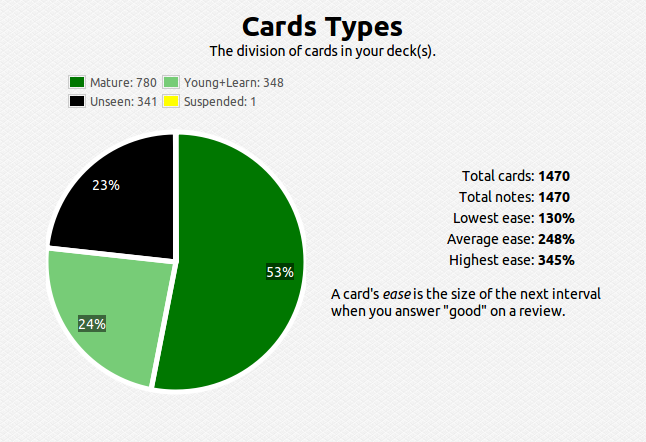
Well, I was inconveniently incapacitated by a cold last week – I fell behind but I managed to catch up on the reading portion by covering four sections over the weekend. The problems take much longer so I’m still behind on that part. I’m hoping to catch up by this weekend, and then maybe use the July 4th weekend to give myself a cushion just in case I fall behind again.
So far, the problems haven’t been too difficult, aside from some proofing problems and some of the application problems that appear at the end of each section. For example, I had to solve the following vector equation with a computer algebra system (as specified in the problem – otherwise most of the problems are to be done by hand):
\[x_1\left[\begin{array}{c} 27.6 \\ 3100 \\ 250 \end{array}\right] + x_2 \left[\begin{array}{c} 30.2 \\ 6400 \\ 360 \end{array}\right] = \left[\begin{array}{c} 162 \\ 23610 \\ 1623 \end{array}\right] \]
Where \(x_1\) and \(x_1\) represent the tons of anthracite coal and bituminous coal burned at a steam plant, with the two vectors on the left side of the equation representing output (heat, sulfur, dioxide, and particulate matter) from burning these two different types of coal, and the vector on the right representing total output. To solve this equation for \(x_1\) and \(x_1\), we can row reduce the corresponding augmented matrix:
\[\left[\begin{array}{rrr} 27.6 & 30.2 & 162 \\ 3100 & 6400 & 23610 \\ 250 & 360 & 1623 \end{array}\right] \]
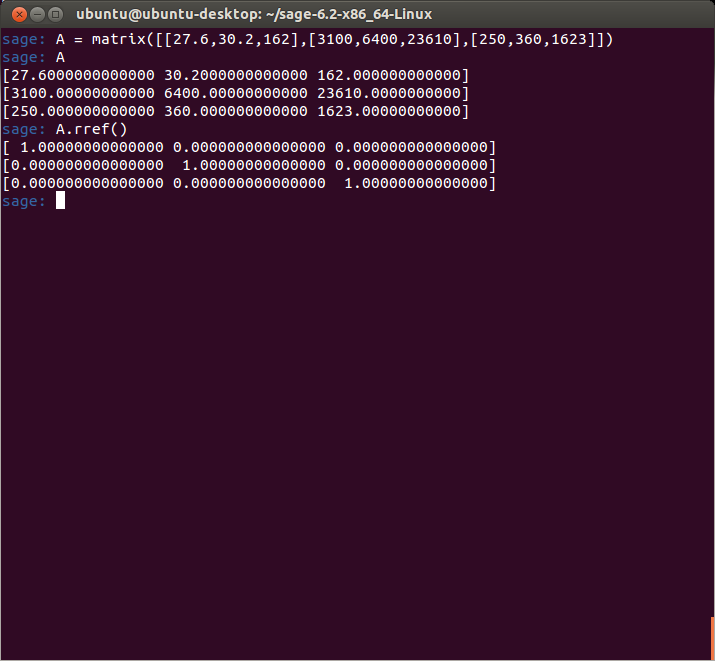
The point of the problem is to determine what amounts of each type of coal are required to produce the given amount of heat and waste product. I thought this would be a straightforward problem to solve, but I ran into some trouble when I tried to row reduce the matrix in sage:
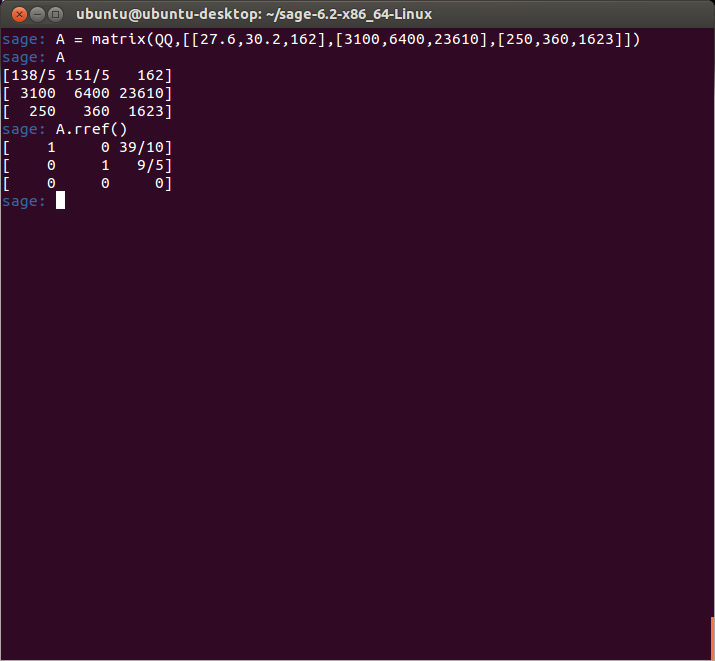
The result above tells me that the system is inconsistent, which to me looked incorrect. I checked my input over and over again for about 30 minutes until I looked up the sage documentation (RTFM, right?) and tried defining the matrix over the ring of rationals (notice the ‘QQ’ in the matrix function below):
Which produced the correct answer. So it looks like I ran into a precision issue in sage. These are some of the things you have to deal with using open source software – if I knew more about this I could try to fix it – but at least with open source software you have the freedom to try.