Monthly Archives: November 2016

You are browsing the site archives by month.

No. 116: 70 Days of Linear Algebra (Day 9)

30 November, 2016 6:51 PM / Leave a Comment / Gene Dan

Section: 1.6 – Applications of Linear Systems

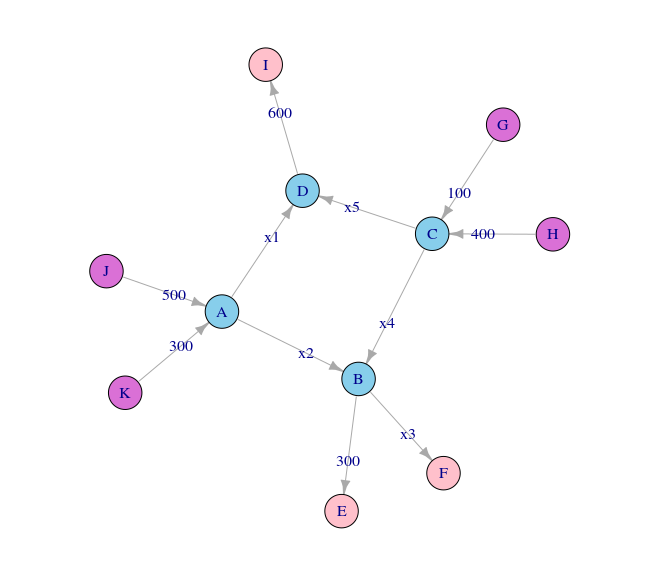
Linear systems can be used to model and solve problems concerning traffic flow. Consider for instance, the following set of intersections modeled by a graph:

The orchid nodes G, H, J, and K represent traffic inflows. The pink nodes E, F, and I represent traffic outflows. The blue nodes A, B, C, and D represent intersections. Each edge (the lines connecting the nodes – representing roads) is labeled with the traffic flow measured in cars per hour. For example, 500 cars travel from J to A each hour. Assuming that for each intersection (and for the network as a whole), that traffic inflow equals traffic outflow, one question arises regarding capacity – how much traffic should the roads x₁, x₂, x₃, x₄, and x₅ be designed to handle?

First, we need to determine traffic inflows and outflows for each intersection:

Intersection	Flow In	Flow Out
A	300 + 500	x₁ + x₂
B	x₂ + x₄	300 + x₃
C	400 + 100	x₄ + x₅
D	x₁ + x₅	600

In addition, we have the constraint that total network inflow (500 + 300 + 100 + 400) equal total network outflow (300 + x₃ + 600), so x₃ = 400.

We can use this information to represent the network as a system of linear equations and row reduce the corresponding augmented matrix to solve for the unknowns:

\[\begin{aligned} x_1+x_2&=800\\x_2-x_3+x_4&=300\\x_4+x_5&=500\\x_1+x_5&=600\\x_3&=400\end{aligned}\]

\[\left[\begin{array}{cccccc} 1 & 1 & 0 & 0 & 0 & 800 \\ 0 & 1 & -1 & 1 & 0 & 300 \\ 0 & 0 & 0 & 1 & 1 & 500 \\ 1 & 0 & 0 & 0 & 1 & 600 \\ 0 & 0 & 1 & 0 & 0 & 400 \\ \end{array}\right] \sim \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 1 & 600 \\ 0 & 1 & 0 & 0 & -1 & 200 \\ 0 & 0 & 1 & 0 & 0 & 400 \\ 0 & 0 & 0 & 1 & 1 & 500 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right] \]

Which leads us to the general solution:

\[\left\{\begin{aligned} x_1 & = 600 – x_5 \\ x_2 &=200+x_5 \\ x_3&=400\\x_4&=500-x_5\\x_5&\text{ is free} \end{aligned}\right.\]

Since x₅ is free, we have infinitely many solutions to the problem. Thus, in practice, how we actually design the roads would depend on how much traffic we anticipate for x₅.

Code used to create the graph

library(igraph)

edges <- c("B","E"
          ,"B","F"
          ,"A","B"
          ,"C","B"
          ,"G","C"
          ,"H","C"
          ,"C","D"
          ,"D","I"
          ,"J","A"
          ,"K","A"
          ,"A","D")

edge_labels <- c("300"
                ,"x3"
                ,"x2"
                ,"x4"
                ,"100"
                ,"400"
                ,"x5"
                ,"600"
                ,"500"
                ,"300"
                ,"x1")

cols <- c("skyblue"
          ,"pink"
          ,"pink"
          ,"skyblue"
          ,"skyblue"
          ,"orchid"
          ,"orchid"
          ,"skyblue"
          ,"pink"
          ,"orchid"
          ,"orchid")
traffic <- graph(x) %>% set_edge_attr("label",value=edge_labels)
traffic$label <- edge_labels
plot(traffic
    ,vertex.color=cols
    ,edge.arrow.size=.4
)

library(igraph)

edges <- c("B","E"

,"B","F"

,"A","B"

,"C","B"

,"G","C"

,"H","C"

,"C","D"

,"D","I"

,"J","A"

,"K","A"

,"A","D")

edge_labels <- c("300"

,"x3"

,"x2"

,"x4"

,"100"

,"400"

,"x5"

,"600"

,"500"

,"300"

,"x1")

cols <- c("skyblue"

,"pink"

,"skyblue"

,"orchid"

,"skyblue"

,"pink"

,"orchid"

,"orchid")

traffic <- graph(x) %>% set_edge_attr("label",value=edge_labels)

traffic$label <- edge_labels

plot(traffic

,vertex.color=cols

,edge.arrow.size=.4

)

Code used to solve the equations

library(pracma)
A = matrix(c(1,1,0,0,0,800
            ,0,1,-1,1,0,300
            ,0,0,0,1,1,500
            ,1,0,0,0,1,600
            ,0,0,1,0,0,400)
            ,nrow=5,ncol=6,byrow=TRUE)
rref(A)

library(pracma)

A = matrix(c(1,1,0,0,0,800

,0,1,-1,1,0,300

,0,0,0,1,1,500

,1,0,0,0,1,600

,0,0,1,0,0,400)

,nrow=5,ncol=6,byrow=TRUE)

rref(A)

Posted in: Mathematics / Tagged: 70 days of linear algebra

No. 115: The Collatz Conjecture

22 November, 2016 7:52 PM / Leave a Comment / Gene Dan

The Collatz Conjecture is a famous unsolved problem in mathematics. Given any positive integer, if that integer is even, divide it by two. If it’s odd, multiply it by three and then add 1. Keep repeating until you get 1. The conjecture claims that no matter what number you start with, you will always reach 1.

Is this the case? Nobody knows! But let’s try a few examples: 12, 7, and 9

12 -> 6 -> 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
9 -> 28 -> 14 -> 7 -> … 8 -> 4 -> 2 -> 1

In all three cases, we get a chain of numbers that eventually leads to 1. In fact, we can try every integer up to 100 million and we will still end up with 1! Given that a counterexample hasn’t been found for extremely large numbers, many people believe the conjecture to be true. The reason why this problem is so famous is because it’s easy to understand, but hard to solve.

Given the example above, we can construct a directed graph that plots each successive step for all situations up to a specified integer. For example, when n = 50:

We can see that every chain leads to 1, which is why so many arrows point to node 1. I’ve created a visualization using R Shiny, and using the slider below, you can see how the graph changes as you change n. I could go on about R Shiny, which is an extremely useful package for visualizing mathematical concepts due to its interactive nature, but since I’m busy, I’ll have to save that for a later time.

The code is contained in 3 files, server.R, ui.r, and helpers.R.

server.R:

library(shiny)
library(igraph)
source("helpers.R")
shinyServer(function(input, output) {
  
  output$distPlot <- renderPlot({
    out.n <- input$n
    pairs <- c()
    for(i in 1:out.n)
    {
      curr <- i
      while(curr != 1)
      {
        if(curr %% 2 == 0)
        {
          nxt <- curr / 2
        }
        else
        {
          nxt <- 3 * curr + 1
        }
        pairs <- c(pairs,as.character(curr),as.character(nxt))
        curr <- nxt
      }
    }
    graph.directed <- graph(pairs)
    l <- layout.forceatlas2(graph.directed, iterations=100,plotstep=0)
    plot(graph.directed,layout=l, vertex.color="skyblue", vertex.size=6, edge.arrow.size=.2, vertex.label.cex=.5)
  })
  
})

library(shiny)

library(igraph)

source("helpers.R")

shinyServer(function(input, output) {

output$distPlot <- renderPlot({

out.n <- input$n

pairs <- c()

for(i in 1:out.n)

{

curr <- i

while(curr != 1)

{

if(curr %% 2 == 0)

{

nxt <- curr / 2

}

else

{

nxt <- 3 * curr + 1

}

pairs <- c(pairs,as.character(curr),as.character(nxt))

curr <- nxt

}

graph.directed <- graph(pairs)

l <- layout.forceatlas2(graph.directed, iterations=100,plotstep=0)

plot(graph.directed,layout=l, vertex.color="skyblue", vertex.size=6, edge.arrow.size=.2, vertex.label.cex=.5)

})

ui.r

library(shiny)

shinyUI(fluidPage(
  
  # Application title
  titlePanel("Collatz Conjecture"),
  withMathJax(
  HTML("Consider the following operation on an arbitrary positive integer:
            <ul>
            <li>If the number is even, divide it by two.</li>
            <li>If the number is odd, triple it and add one.</li>
            </ul></br>
  In modular arithmetic notation, define the function \\(f\\) as follows:</br>
$$f(x)= \\left\\{
\\begin{aligned}
     \\ n/2  &\\quad  \\text{if } n\\equiv0\\,(\\text{mod } 2)  \\\\
     \\ 3n+1 &\\quad  \\text{if } n\\equiv1\\,(\\text{mod } 2)  \\\\
     \\end{aligned}
     \\right.$$
  Now, form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next.
       In notation:
$$a_i=\\left\\{
       \\begin{aligned}
       \\ n          & \\quad \\text{for } i = 0 \\\\
       \\ f(a_{i-1}) & \\quad \\text{for i} >0 \\\\
       \\end{aligned}
       \\right.$$
  The Collatz conjecture is: <i>This process will eventually reach the number 1, regardless of which positive integer is chosen initially</i>.")),
  
  # Sidebar with a slider input for K 
  sidebarLayout(
    sidebarPanel(
       sliderInput("n",
                   "Directed graph for all sequences up to n:",
                   min = 2,
                   max = 100,
                   value = 50)
    ),
    
    
    mainPanel(
       plotOutput("distPlot",width="500px", height="500px")
    )
  )
))

library(shiny)

shinyUI(fluidPage(

# Application title

titlePanel("Collatz Conjecture"),

withMathJax(

HTML("Consider the following operation on an arbitrary positive integer:

<ul>

<li>If the number is even, divide it by two.</li>

<li>If the number is odd, triple it and add one.</li>

</ul></br>

In modular arithmetic notation, define the function \$f\$ as follows:</br>

$$f(x)= \\left\\{

\\begin{aligned}

\\ n/2 &\\quad \\text{if } n\\equiv0\\,(\\text{mod } 2) \\\\

\\ 3n+1 &\\quad \\text{if } n\\equiv1\\,(\\text{mod } 2) \\\\

\\end{aligned}

\\right.$$

Now, form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next.

In notation:

$$a_i=\\left\\{

\\begin{aligned}

\\ n & \\quad \\text{for } i = 0 \\\\

\\ f(a_{i-1}) & \\quad \\text{for i} >0 \\\\

\\end{aligned}

\\right.$$

The Collatz conjecture is: <i>This process will eventually reach the number 1, regardless of which positive integer is chosen initially</i>.")),

# Sidebar with a slider input for K

sidebarLayout(

sidebarPanel(

sliderInput("n",

"Directed graph for all sequences up to n:",

min = 2,

max = 100,

value = 50)

mainPanel(

plotOutput("distPlot",width="500px", height="500px")

)

))

The helpers.R file was taken here, and was used to apply the ForceAtlas 2 layout on the igraph package.

Posted in: Mathematics

Monthly Archives: November 2016

No. 116: 70 Days of Linear Algebra (Day 9)

No. 115: The Collatz Conjecture

Archives

Categories

Links

Texas Cycling