Monthly Archives: July 2017

You are browsing the site archives by month.

No. 119: 25 Days of Network Theory – Day 2 – Matrix Representations of Networks

5 July, 2017 7:39 PM / Leave a Comment /

Visualizations of networks can look pretty, but of course without a formal mathematical language to describe the properties of these networks, we will not be able to quantitatively answer the questions we would like to have answered about such networks. Today I’ll introduce two ways of defining networks in terms of matrices – adjacency matrices and incidence matrices, which connects the ideas of network theory with those of linear algebra.

Adjacency Matrices
Suppose G=(V,E) is a simple network where V={1,2,\ldots,n}.
For 1\leq i,j\leq n define

    \[a_{ij}=\left\{\begin{aligned} 1, & \quad (i,j)\in E, \\ 0, &\quad (i,j)\not\in E.\end{aligned}\right.\]

Then the square matrix A=(a_{ij}) is called the adjacency matrix of G.

Adjacency matrices are a way to define networks from the perspective of their nodes. The notation above simply specifies a square matrix whose rows and columns correspond to the nodes of the network. The each entry will be 1 if there is an edge connecting its corresponding row and column (which represent nodes) and 0 otherwise.

Going back to our Les Miserables example, the graph below:
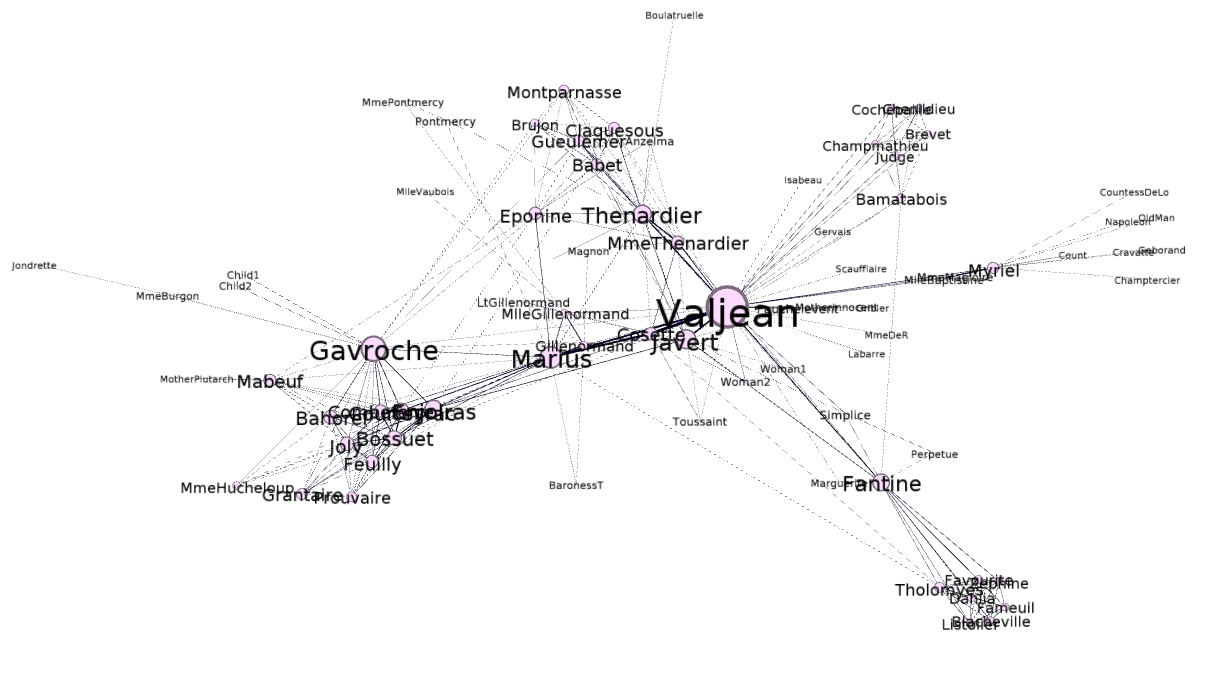
Selection_266

Is represented by the following adjacency matrix:
Selection_267

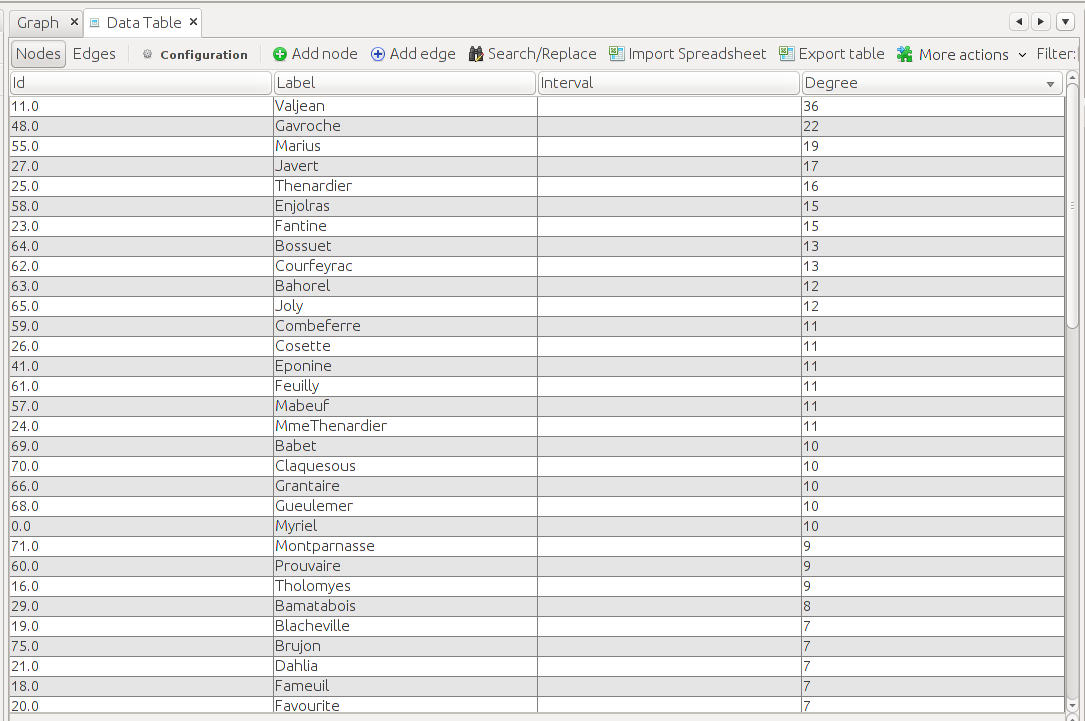
Here, the column names are omitted, but they should follow the same order as the row names. If you add up the 1s in a row, the sum should be equal to the degree of the node that it represents. For example, the sum of the row that represents Jean Valjean (highlighted in the matrix above) equals 36. This is both consistent with the data from gephi and the theory represented in the text:

Selection_268

Furthermore, we can see that certain characters who are connected with Myriel have a degree of 1, such as Napoleon, Cravatte, and Champtercier, which are seen in both the matrix and the visual representation of the graph if we zoom in:
Selection_271

A short script was used to import the gexf data, convert it into an igraph object, and from there calculate and print the adjacency matrix.

Incidence Matrices

Suppose G = (V,E) is a network where V={1,2,\ldots,n} and E={e_1,e_2,\ldots,e_m} with e_i=(u_i,v_i).
For 1\leq i\leq m and 1\leq j \leq n define

    \[b_{ij}=\left\{\begin{aligned} 1, & \quad u_i=j, \\ 1, &\quad v_i = j, \\ 0 & \quad \text{otherwise.}\end{aligned}\right.\]

Then the rectangular matrix B=(b_{ij}) is called the incidence matrix of G.

Incidence matrices are a way to define networks from the perspective of edges. The notation above simply means that this time, we’ll have a matrix whose columns represent each edge in the network, and the rows represent nodes. Each entry will be a 1 if the character represented by a row participates in the edge represented by the column, and zero otherwise.

Unfortunately, igraph (at least to my knowledge) can’t calculate the incidence matrix for a nonbipartite graph, so I had to use a workaround I found on stackoverflow. I’ve also altered the in the definition from the original text to be consistent with this workaround (the original had a -1 for the v’s).

The LesMiserables network has 77 nodes and 254 edges, so we’ll have a very wide matrix that is too large to display on this webpage. However, I’ve added a screenshot to give just a glimpse as to what it looks like:
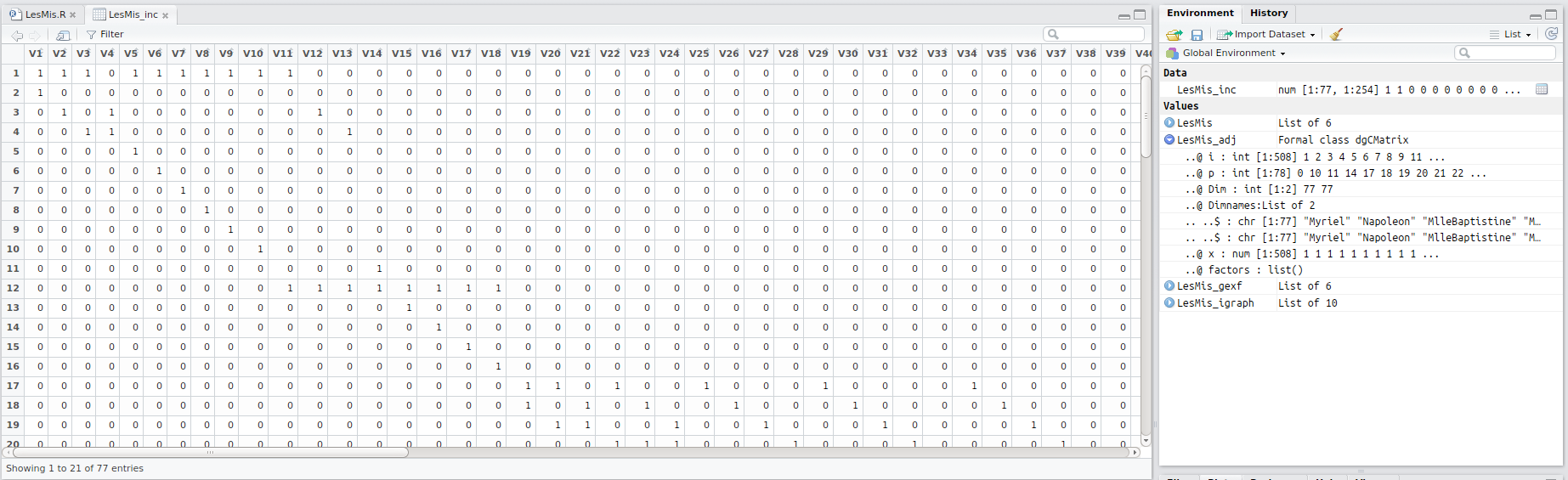
Selection_273
The code used to generate the matrix:

Posted in: Mathematics

No. 118: 25 Days of Network Theory – Day 1 – Introduction

5 July, 2017 11:14 AM / Leave a Comment /

Selection_265
I’ve decided to dedicate this month to the study of network theory. For the past few years, I’ve been intrigued not only by the theory’s simplicity – that a graph is simply a collection of nodes and edges, but also its ability to answer seemingly complex and qualitative questions regarding society (both human and nonhuman) in general, such as:

  • Who are the most influential members of society?
  • What are the most natural subdivisions for identifying communities within a population of people?
  • How can we construct a transportation system that optimizes traffic flow and minimizes traffic jams?
  • How can small disruptions spread through a network to cause financial crises?
  • How can we quantify consensus?
  • How are social norms and reputational effects enforced?
  • How quickly can a disease spread throughout a community?

…and so on.

At first glance, the above graph may not look like anything special – but there is indeed something very special about it. This network represents co-occurrences between characters in Victor Hugo’s Les Miserables. After we add some labels to identify the characters, and adjust the size of the nodes and labels to reflect the degree (that is, the number of edges a node participates in), the graph becomes more meaningful in that you can immediately identify the most important characters to the plot:

Selection_266

You can see that the largest node is represents Jean Valjean, the main protagonist of the story. This means that, at least according to degree, Jean Valjean is the most important person in the novel. However, there are several other quantitative measures of influence, and we will later see that Jean Valjean may not be the most influential character in the book, at least according to those other measures.

For this course, I’ll be reading Estrada and Knight’s, A First Course in Network Theory, and I’ll be reading 10 pages per day and applying what I learned there to the Les Miserables network.

There wasn’t much to the first ten pages other than to introduce the history of graph theory (there was a section on the Seven Bridges of Königsberg). So, I’ve used this opportunity to introduce what tools I’ll be using for the course of study. There’s gephi, a graph visualization program, igraph, a package that I’ll be using to perform more quantitative analyses on this network in R, and the Les Miserables network dataset itself.

Posted in: Mathematics