Oftentimes, we would like to think about the connectivity of a network, that is, how robust is a network to the removal of nodes and edges? I can think of several real-world applications where we might ask this question, for example:
- Which roads can we remove from the transportation network such that people can still get to where they want to go?
- Which metro stations would cause the most disruption to the network if they were destroyed?
- What enemy bases should we target first if we want to disrupt their supply chain?
- Where should we add roads, or other links between stations to increase the robustness of the network?
- What would happen to a group of friends if certain people left? Would they still hang out?
…and so on.
This brings us to two measures of network cohesiveness – edge connectivity and vertex connectivity. Simply stated, edge connectivity measures the number of edges we would need to remove from a network in order to divide it into distinct components. For example, think about your daily commute. If we were to remove one of the roads on your commute, you would probably still be able to reach your destination, even though you’d have to find some other way to get to work. However, if we were to remove more and more roads, eventually you would be unable to get there, and at some point, if we remove even more roads, your workplace may become an inaccessible island separate from the rest of the transportation network. We would call your workplace a component, that is, a node unreachable from any other node. Edge connectivity measures the minimum number of edges we would have to remove in order to separate a network into distinct components. The higher the edge connectivity, the more edges we’d have to remove – so we can say that the higher this number, the more cohesive the network is.
Formally,
Suppose 
is a simple network.
- A disconnecting set of
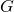is any subset 
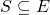for which the network 
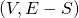has more components than 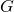. - S is a cut-set of 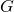if it contains no proper subsets that are disconnecting sets.
- The edge connectivity of a network 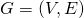is the number of edges in the smallest cut-set and is denoted by
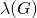. If 
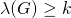then 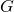is k–edge connected.
Formally, a set of nodes in a connected network is called a separating set if their removal (and the removal of incident edges) disconnects the graph. If the smallest such set has size k then the network is called k–connected and its connectivity, denoted 
, is k. If 
then a node whose removal disconnects the network is known as a cut-vertex.
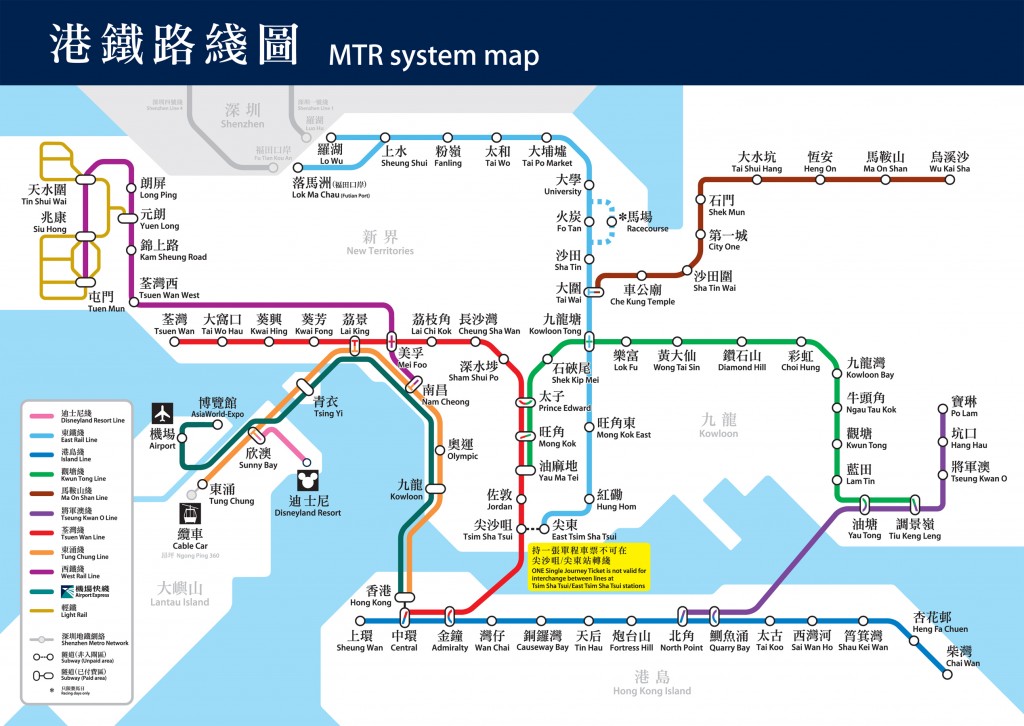
Likewise, vertex connectivity measures the number of nodes we’d have to remove (along with their associated edges) in order to separate a network into distinct components. For example, consider the Hong Kong subway system:
If you ever have the chance to ride the subway in Hong Kong, I recommend that you do – in my mind it’s the best subway system in the world. In network theory, we call this type of network a connected graph, that is, every subway station is reachable from every other station. If we were to remove Wong Tai Sin from the map, we’d still be able to reach every station from every other station. Likewise, we’d still be able to do so if we removed the stations on the periphery, like Chai Wan or Wu Kai Sha. However, if we were to remove just a single important station, say Quarry Bay, we would sever the eastern portion of the Island Line from the rest of the network. Thus, Quarry Bay is a cut-vertex of the Hong Kong subway system. Since vertex connectivity measures the minimum number of nodes we’d have to remove to separate a graph, we say that Hong Kong’s subway system has a vertex connectivity of 1. Like edge connectivity, the higher the vertex connectivity, the more robust the network.
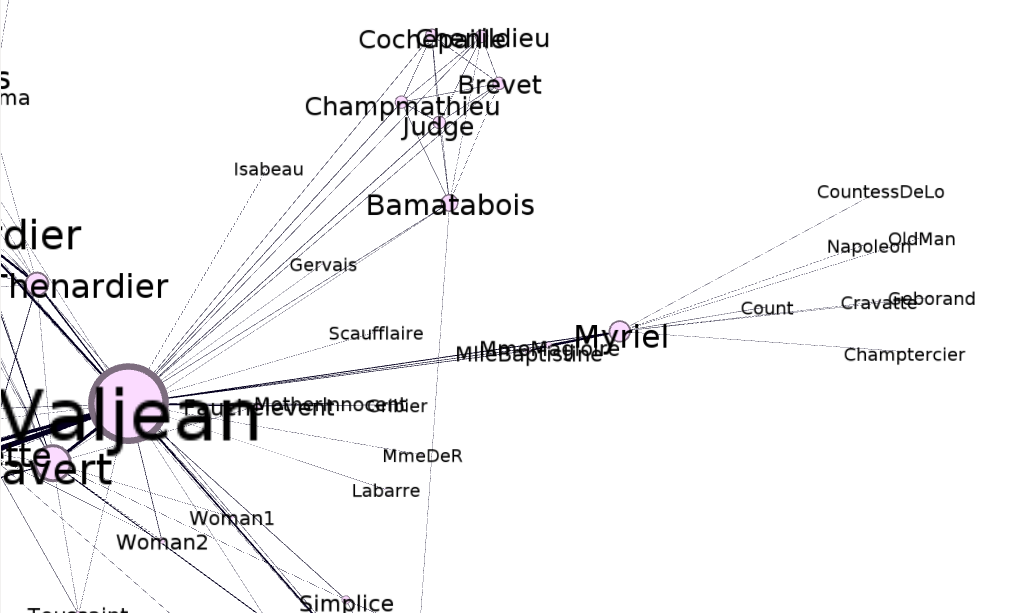
Looking at our Les Miserables example, it’s pretty obvious that both the edge and vertex connectivity is one:
If we were to remove the edge between Myriel and Napoleon, we would separate the graph. Likewise, if we were to remove Myriel from the picture, we’d also separate the graph. This is a somewhat boring example, and output from the R console confirms this is true:
|
1 2 3 4 5 6 7 8 9 10 |
> #Import gexf file and convert to igraph object > LesMis_gexf <- read.gexf("LesMiserables.gexf") > LesMis_igraph <- gexf.to.igraph(LesMis_gexf) > > #Calculate edge and vertex connectivity > edge_connectivity(LesMis_igraph) [1] 1 > vertex_connectivity(LesMis_igraph) [1] 1 > |
However, one neat thing the igraph package can do is determine the separating sets of minimum size that separate a network. The terminology is a bit different in the igraph documentation, but I was able to find a function that identifies what are called separators. It turns out there are several such separators in our example, and because the vertex connectivity of this network is 1, R returns 8 cut-vertices from the network:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
> min_separators(LesMis_igraph) [[1]] + 1/77 vertex, named: [1] Valjean [[2]] + 1/77 vertex, named: [1] Fauchelevent [[3]] + 1/77 vertex, named: [1] MmeBurgon [[4]] + 1/77 vertex, named: [1] Gavroche [[5]] + 1/77 vertex, named: [1] MlleGillenormand [[6]] + 1/77 vertex, named: [1] Mabeuf [[7]] + 1/77 vertex, named: [1] Thenardier [[8]] + 1/77 vertex, named: [1] Myriel |
There are some weaknesses to this approach. Just because the removal of a node disconnects a network doesn’t mean we shouldn’t remove such a node in a real world application. If node served as a connection to unimportant parts of a network it may be wise to remove it if the costs of maintaining such a node outweighed the benefits. I’m hoping that tools to address issues such as this will be introduced further along in the course.