Hey everyone,
Today I thought of a small coding exercise for me to do to work on algorithm building – I decided to write a program that converts positive decimal numbers to binary numbers. I knew that I could probably find plenty of examples on the web of this algorithm, but I decided to find out for myself how the conversion worked before looking for any help. Anyhow, one method of algorithm discovery involves the application of that algorithm to a specific example known to be true, and then using that example to pick apart the steps. What I mean is that many of us use algorithms every day in order to solve problems without realizing it or understanding it. For instance, most of you have probably used the division algorithm daily ever since you learned it in kindergarten – for instance, to divide 7 by 2 we subtract the product of 3 and 2 from 7 to obtain the remainder 1. Thus, 7 divided by 2 equals 3 remainder 1. However, how do we know that this algorithm works every single time for every pair of integers? Fortunately prior math enthusiasts have given us a logically rigorous explanation. Looks more complicated when printed, right?
Now, let’s examine how to find the binary value of the integer 27. First, let me give a brief description on how binary values work. In the binary system, every digit of a number is represented by either 1 or 0, in contrast to our common base-10 system, or decimal system, in which each digit may be represented by 0,1,2,3,4,5,6,7,8, or 9. For instance 1 in base-10 is 1 in base-2, 2 in base-10 is 2 in base-2, 3 in base-10 is 11 in base-2, 4 in base-10 is 100 in base-2, and so on, and so forth. In base-2, 10 is twice as much as 1, 100 is twice as much as 10, 1000 is twice as much as 100, and in this manner each digit represents a unit that is twice as large as the digit to the right of it. Check out the link on the binary system to learn more.
Let’s go back to 27. You could try counting in binary (1, 10, 11, 100, 101, …) but that would take too long and would be cumbersome to program. An alternative method we could try is to break up the number 27 into different binary unit values (1000’s, 100’s, 10’s, 1’s), add them up and obtain the final binary representation. However, how many digits would the resulting binary number be? We can’t deduce the answer simply by staring at 27, so let’s try to divide by 2 and see what happens. After dividing 27 by 2, we get 13 remainder 1. What happens if we divide 13 by 2? We get 6 remainder 1. Dividing 6 by 2 gives us 3, and dividing 3 by 2 gives us 1 remainder 1. Note that we applied the division algorithm 4 times. It just so happens that 2^4 = 16, and that 10^4 = 10000. We know that 10000 in binary is equal to 16 in decimal because 10 in binary is equal to 2 in decimal and 10x10x10x10 in binary is equal to 2x2x2x2 in decimal. Thus, we know that 16 out of our original 27 consists of 10000 in binary. What about the other 27 – 16 = 11? We then take 11 and divide that by 2 to obtain 5 remainder 1, divide 5 by 2 to obtain 2 remainder 1, and divide by 2 to obtain 1. In this next round of divisions we have applied division by 2, 3 times. Thus 10x10x10 = 1000 in binary, which is equal to 8 in decimal. Now we have 11-8 = 3 remaining to consider. We divide 3 by 2 to obtain 1 remainder 1. We have applied division by 2 once, so 10 in binary is equal to 2 in decimal. Now we only have 3-2 = 1 remaining and 1 in decimal is equal to 1 in binary. So, we know that 16 + 8 + 2 + 1 in decimal is equal to 10000 + 1000 + 10 + 1 = 11011 in binary…success!
I must stress that this does not prove that the algorithm works – it has only worked in this one particular instance. However, this instance has shed some light, at least for now until I actually gain the knowledge to do a mathematically rigorous proof – which won’t be coming in a long time!
Using this example as a guide I wrote down some code:
[sourcecode language=”css”]
//Decimal to Binary Conversion
#include <iostream>
#include <cmath>
using namespace std;
const int base = 2;
long long baseconv(long);
int main()
{
long long inputval;
cout << "Enter an integer: _b";
cin >> inputval;
cout << inputval << " is " << baseconv(inputval) << " in binary!" << endl;
return 0;
}
long long baseconv(long input)
{
long long baseconv;
long long updater;
long long dival;
long digitcount;
baseconv = 0;
while (input > base – 1)
{
digitcount = 0;
dival = input;
while (dival > base – 1)
{
dival = dival / 2;
digitcount = digitcount + 1;
}
updater = pow(base, digitcount);
baseconv = baseconv + (pow(10,digitcount));
input = input – updater;
}
baseconv = baseconv + input;
return baseconv;
}
[/sourcecode]
Here’s an example of the output:
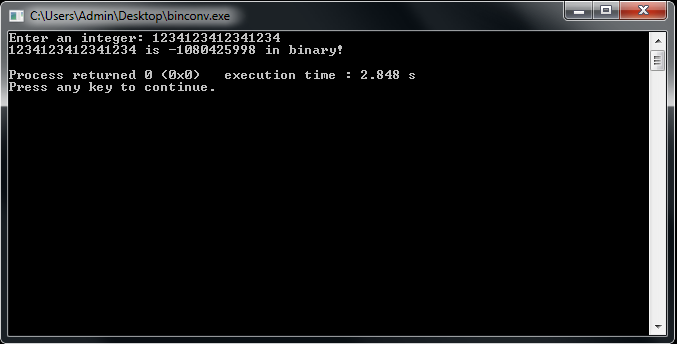
I’m running out of time so I don’t want to go into every single detail over this program, but in a nutshell, the program splits the input integer into separate binary parts, then adds the binary parts together in order to obtain the result. Unfortunately, the memory limitations of c++ do not allow me to convert very large integers, such as 1234123412341234. See what happens when I try to convert this value:
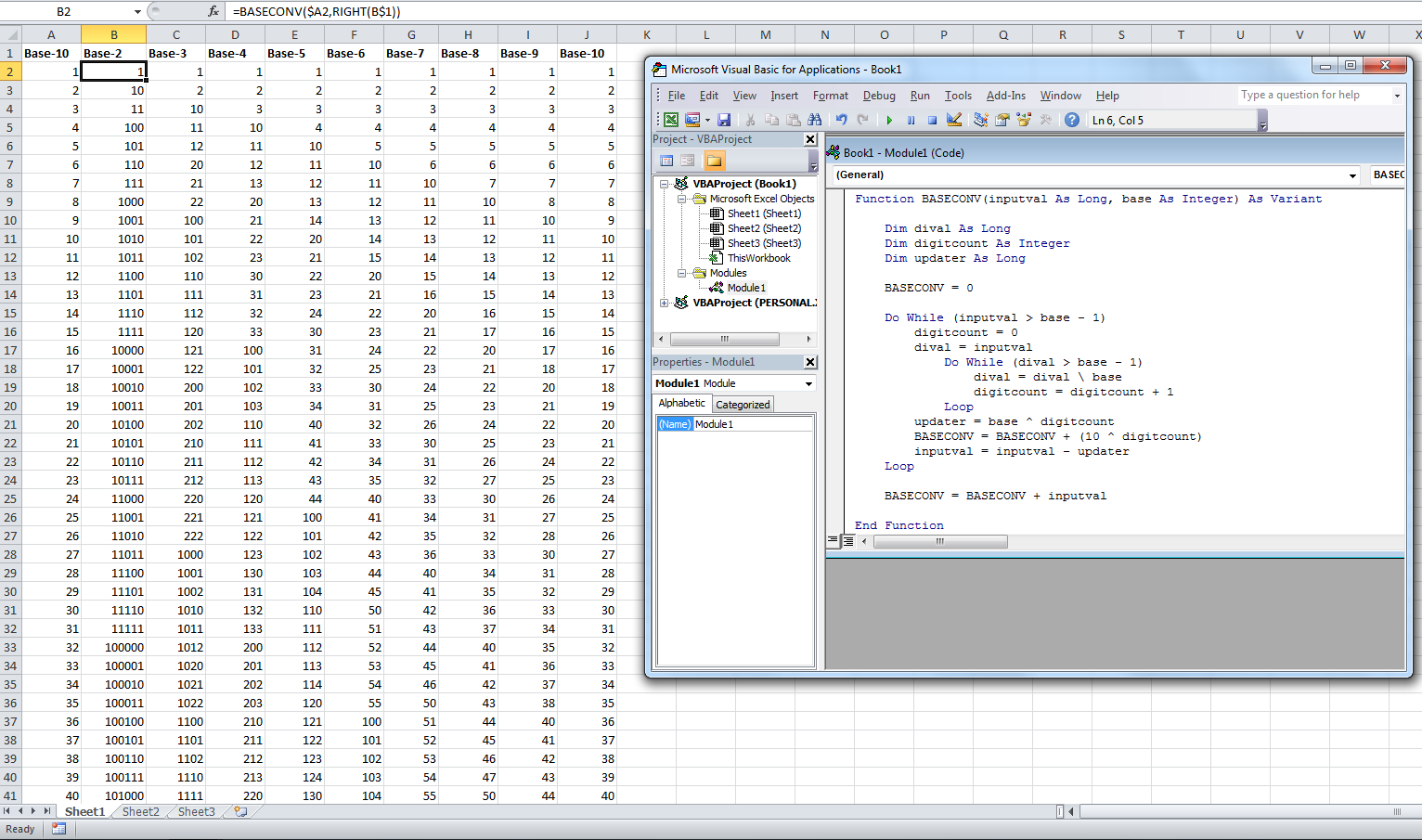
Also, the program does not work with negative values, so those will be two things that I will work on in the near future. I also spent the time to port the program into VBA, and I changed it to do conversions from base-10 to any base the user chooses:
[sourcecode language=”css”]
Function BASECONV(inputval As Long, base As Integer) As Variant
Dim dival As Long
Dim digitcount As Integer
Dim updater As Long
BASECONV = 0
Do While (inputval > base – 1)
digitcount = 0
dival = inputval
Do While (dival > base – 1)
dival = dival base
digitcount = digitcount + 1
Loop
updater = base ^ digitcount
BASECONV = BASECONV + (10 ^ digitcount)
inputval = inputval – updater
Loop
BASECONV = BASECONV + inputval
End Function
[/sourcecode]
Notice how much more efficient the code is! That’s because VBA is at a much higher level than C++, so there are a lot more built-in functions that do the work for you. Here’s an example of the output: