Author Archives: Gene Dan

No. 101: Visualizing Networks

25 December, 2013 11:06 PM / 4 Comments /

Hello,

Today I’d like to give a brief update on some of the things I’ve been working on over the past few months, and perhaps briefly cover some projects that I’ve planned for myself for the upcoming year.

Networks

A few months back, an actuary contacted me and asked me if I wanted to study network analysis. I had looked into the subject a year ago and even bought some books (Networks by Mark Newman and Networks, Crowds, and Markets by Easley and Kleinberg), but never got around to reading them. Last week, I finally started reading the Easly and Kleinberg text, and right now I’m in the early stages covering basic terminology.

In short, the study of networks is a combination of graph theory and game theory, and is used to study crowd behavior and things like conformity, political instability, epidemics, and market collapse. These things have interested people for some time as they are social phenomena that have, from time to time, led to social upheaval and destruction.

Visualization

Over the past decade, the amount of data that we have on social networks has grown exponentially, and so has computing power. This has now made the empirical analysis of networks, which was once impractically expensive and time-consuming, possible. I’ve initiated a project called hxgrd which will essentially serve as a platform for simulating discrete, turn-based behavior amongst crowds. I’ve only initialized the repository (I’ll talk more about this github project in another post), and I’m looking for some software that I can integrate into the platform to save me some time later on.

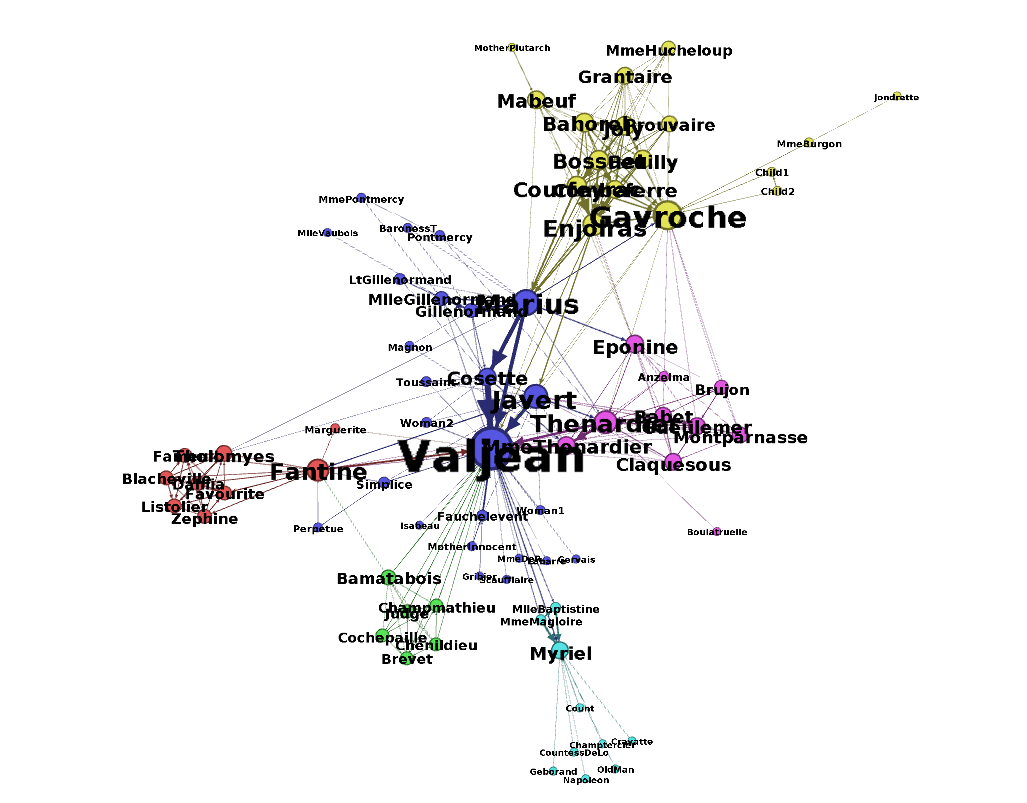
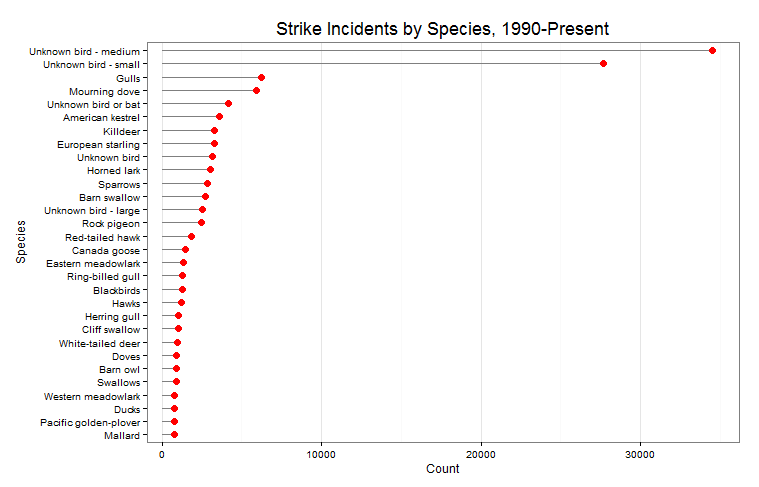
I stumbled accross a software called gephi which is an open-source tool used to visuzlize and analyze networks. I downloaded the program out of curiosity and went through their tutorial, which invovles visualizing the relationships between characters of Les Misérables (perhaps you have read the book or seen the musical). Here is a chart generated by gephi:

Selection_064 (copy)

The graph consists of circles, called nodes, and lines connecting these nodes, called edges. Each circle represents a character that appears in the novel. Each line represents an association between characters. The size of the circles and names of the characters vary proportionally with the number of connections that a character has. As you can see here, Jean Valjean, the main character, has the greatest number of connections.

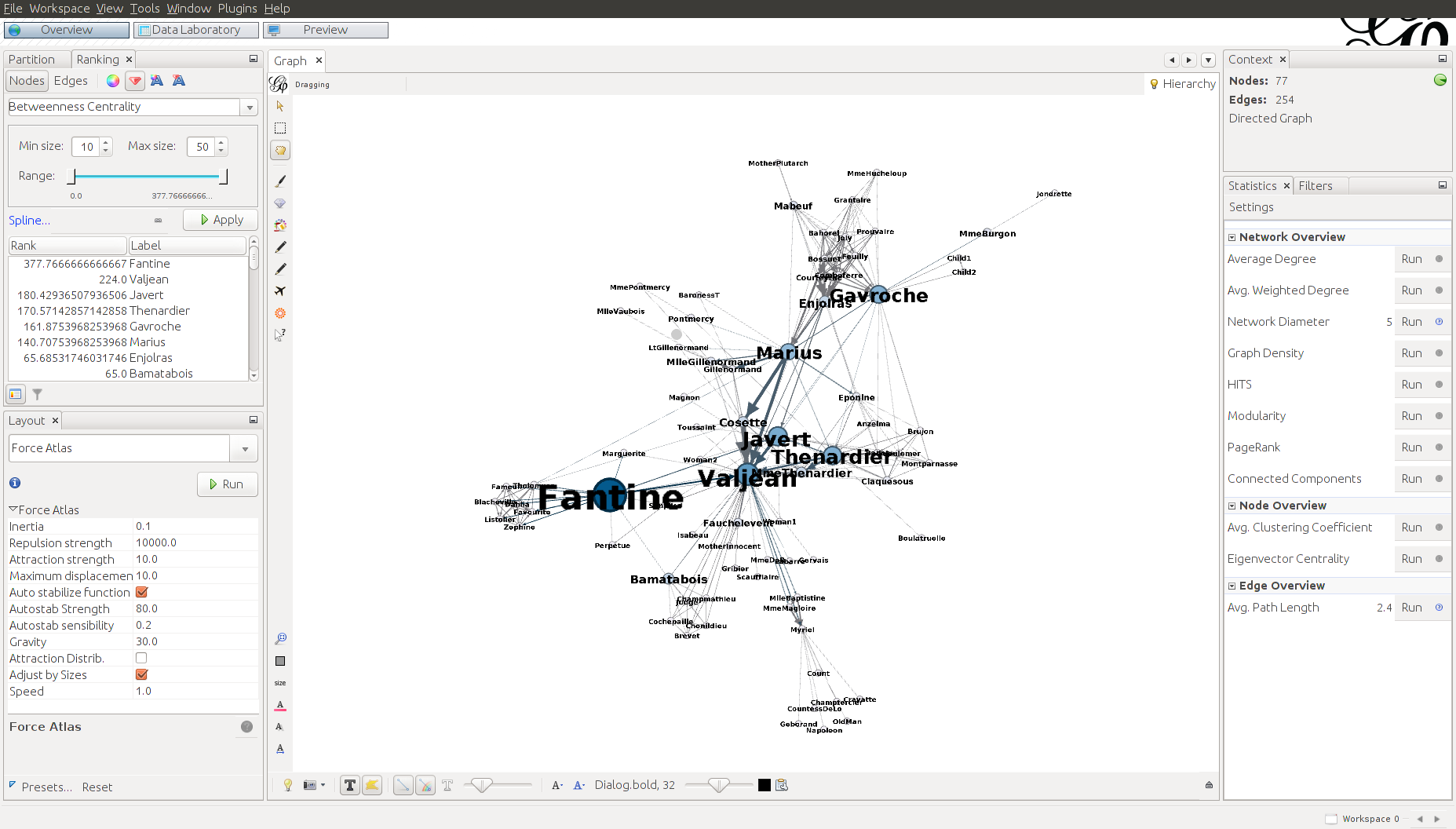
However, just because a character has the most connections doesn’t mean they are the most influential, and an alternative measure, called betweenness centrality, is a measure of a node’s importance. Below, we can see that Fantine has the highest betweenness centrality:

Selection_063 (copy)

Gephi can also determine the groups to which characters belong, denoted by color:

Selection_065

The dataset that was used to generate these diagrams is in XML format:

LesMiserables.gexf (~-Desktop) - gedit_066

And below you can see what the complete GUI looks like:

Gephi 0.8.2 - Project 0_062

Well that’s it for today! I’ll look into the software to understand how it works and to see if I can integrate parts of it into my hxgrd project.

Posted in: Mathematics / Tagged: , , , ,

No. 100: Strike Incidents – Visualizing Data with ggplot2

17 October, 2013 7:55 PM / Leave a Comment /

Today, I’d like to demonstrate some of ggplot2‘s plotting capabilities. ggplot2 is a package for R written by Hadley Wickham, who teaches nearby at Rice University. I’ve been using it as my primary tool for visualizing data both at work and in my spare time.

Wildlife Strikes

The Federal Aviation Administration oversees regulations concerning domestic aircraft. One of the interesting things they keep track of are collisions between aircraft and wildlife – the vast majority of which involving birds. This dataset is available for download from the FAA website.

It turns out that bird strikes happen a lot more frequently than I thought. A quick look at the database revealed that 146,607 reported incidents have occured since 1990 (about 11,000 per year), with the number of birds killed ranging anywhere from 1 to over 100 per incident (cases in which an airplane flew through a flock of birds). Although human deaths are infrequent (less than 10 per year), bird strikes cause substantial physical damage at around $400 million per year

ku-bigpic

An example of bird-related damage.

Data Preparation
There are tools available that allow R to communicate with databases via ODBC connectivity. The database concerning strike incidents is in .mdb format which can be accessed with the package RODBC.

The code below loads the package RODBC along with ggplot2 and returns a brief summary of our dataset:

str

As you can see, data in this form are not easy to interpret. R’s visualization tools allow us to transform this data into something meaningful for our audience.

RODBC lets us send SQL queries to the database connection to aggregate and summarize the data. I found MSAccess’ particular SQL implementation to be very awkward, but I was able to alter my code enough to succesfully return the number of incidents by year:

stryr

Next, we use the function ggplot from ggplot2 to create a bar plot of our data:

strike_yr

From the diagram above, we can see that the number of strikes has increased substantially over the last 24 years. However, we can’t make any definite conclusions without more information. Perhaps this increase is due to more aircraft being flown for longer durations. Or maybe it’s due to better/more accurate reporting of incidents. Notice that the bar for 2013 is much lower than the previous year. The most straightforward explanation for this observation is that 2013 isn’t over yet, and not all the incidents that have happened have been reported yet.

We can use ggplot2 to see the proportion of strikes that have been incurred by the military. The fill argument specifies that the bars should be segmented by operator type:

strike_militry

Now, let’s take a look at which aircraft operators have experienced the most accidents over the last 24 years. The code below sends a query to the database connection that summarizes the incidents by operator:

oper

In this case, the data were not ordered upon extraction, so the two lines after the SQL query reorder the strikes.oper vector by strike count.

We can now use this data to visualize the top 30 operators with a dot plot:

strike_oper

It turns out United Airlines happens to have the most incidents, followed by an ambiguous class called “Business” (perhaps private aircraft), the military, and Southwest Airlines. Keep in mind that this says nothing about the frequency of such incidents, only the magnitude. We’ll need more data in order to make inferences about things like safety. It could be the case that United and Southwest are relatively safe airlines, but only have many incidents because they fly the most hours.

So, which animals happen to have the most strike incidents? The code below summaries the data and plots it in a dot plot:

strike_spec

Most of the time, the type of animal is unidentifiable (go figure), but when it is the most likely case is that it’s a gull or a mourning dove. There are many more species in the database than are depicted in the chart above, which only has the top 30. Below is a partial list of species:

spec

Interestingly, I saw some land animals in the dataset, such as elk, caribou, and aligators (not shown above, but you can see coyotes).

Posted in: Logs, Mathematics / Tagged: , , , , , ,

No. 99: Eratosthenes’ Sieve

26 August, 2013 8:29 PM / Leave a Comment /

A friend of mine pointed out that I had skipped a few steps in the solution I posted yesterday for Euler #3 – first, I didn’t actually go through the process of finding the primes, and second, I didn’t try to figure out how many prime numbers would be necessary for the list I used to find the largest prime factor of 600,851,475,143. To rectify these issues, I wrote another program that can provide the general solution for any integer larger than 1:

All you have to do is replace 600,851,475,143 with a number of your choice, and the script above will find the largest prime factor for that number, given enough time and memory. I was actually somewhat lucky that the answer ended up being 6857. Had it been larger, the program might have taken much longer to execute (possibly impractically long if the factor happened to be big enough).

Eratosthenes’ Sieve

Now that I have that out of the way, I would like to demonstrate a method for quickly generating prime numbers, called Eratosthenes’ Sieve. You can embed this algorithm into the solution of any Project Euler problem that calls for a large list of prime numbers under 10 million (after 10 million, the algorithm takes a long time to execute, and other sieves may be a better choice). While it’s possible to generate prime numbers on the fly for Euler problems, I still prefer to use lists to solve them. Below is the algorithm for Eratosthenes’ Sieve that I’ve written in R:

The script above will generate a list of all the primes below 10,000,000. The algorithm starts with a list of integers from 2 to 10,000,000. Starting with 2, the smallest prime, you remove all the multiples of 2 from the list. Then you move on to the next prime, 3, and remove all the multiples of 3 from the list. The process continues until the only numbers left in the list are prime numbers.

primes2

As you can see, all the composite numbers are now marked as zeros. The final line of the script removes these zeros and gives you a list of just the prime numbers.

primes3

Posted in: Mathematics / Tagged: , , , ,

No. 98: Project Euler #3 – Largest Prime Factor (solution in R)

25 August, 2013 1:15 PM / 1 Comment /

Question:

The prime factors of 13195 are 5, 7, 13 and 29.

What is the largest prime factor of the number 600851475143 ?

Approach:

Every integer greater than one has a unique prime factorization. This means that each integer greater than one can be represented as a unique product of prime numbers. For example, the number 5,784 can be written as:

\[2^3\times 241\]

Where 2 and 241 are prime. Likewise, the number 54,887,224  can be written as:

\[2^3\times 7 \times 53 \times 18493\]

Where 2, 7, 53, and 18493 are prime. For this problem, our goal is to find the largest prime factor of the number 600,851,475,143. An interesting thing to note is that the mathematician F. N. Cole, back in 1903, found the prime factorization of the number 147,573,952,589,676,412,927, which is 193,707,721 × 761,838,257,287. It took him three years worth of effort to do so. While our number is not quite as large as Cole’s, such problems today are trivial. Computer algebra systems such as Mathematica can factorize large numbers very quickly. What took Cole 3 years back in 1903 now takes less than a second today.

We have some discretion in our approach to solving this problem. You can probably use Mathematica to solve it with a single line of code. On the other hand, if you’re using a bare programming language like C++, you would probably need to write more code. Your choice on what to do depends on what you want to learn from solving the problem. I had previously solved this problem using VBA which first involved creating a list of prime numbers, using the list to find the prime factors of 600,851,475,143, and then selecting the largest one as my answer. With R, I’ve taken a middle approach, compromising between arriving at an immediate answer with a computer algebra system and having to create a list of primes from scratch. In this case, I used a list of primes I found off a website and saved them into a file called primes.csv. My mental outline is as follows:

1. Obtain a list of prime numbers
2. Find which of these prime numbers divide 600,851,475,143 evenly.
3. Of the primes that divide 600,851,475,143 evenly, find the largest one.

Solution:

The first line does five things. First, it imports the list of prime numbers as a data frame, then converts the data frame into a matrix, then converts the matrix into a vector, and then sorts the primes within the vector in ascending order. This vector is then assigned to the variable primes. The second line accomplishes three things. The which() function returns the indices of the elements that divide 600,851,475,143 evenly. These indices are then used to extract the corresponding elements of the vector primes. Finally, the function max() returns the largest of these primes, giving us the answer, 6857.

I thought this answer would avoid the tedium of having to calculate each prime myself, but was not so trivial that I could find the answer without learning anything. I thought this method was a good way to demonstrate the use of indexing to find the solution.

Posted in: Mathematics / Tagged: , , , , ,

No. 97: Project Euler #2 – Even Fibonacci Numbers

19 August, 2013 6:54 PM / Leave a Comment /

Question:

Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.

Background:

There are some interesting things to note about Fibonnaci. Students often get their first introduction to the Fibonacci numbers when they first learn about sequences. The popular story is that they were used by Fibonacci to model rabbit populations over a period of time – you start with one pair of rabbits, denoted by 1 as the first term of the sequence. After a month, this pair of rabbits produces another pair, and now the total number of pairs is two. After another month, these two pairs produce another pair, resulting in a total of three pairs after two months. After three months, these three pairs produce 2 additional pairs, resulting in a total of five. The sequence then continues indefinitely, and students are often surprised at how quickly the terms grow.

Beyond the Fibonnaci numbers, there are some more interesting things about the mathematician for whom they are named, and how he fits in with the history of mathematics. While the Fibonacci numbers may be the most widespread way in which people are aware of Fibonacci’s existence, they are not (at least in my opinion), his most important contribution to western mathematics. Although the Fibonacci numbers appear in his book, Liber Abaci, the book itself also introduces the Hindu-Arabic number system, and it was this book that played a crucial role in popularizing the Arabic numerals – the numbers we use today – in western society. Prior to that, Europeans relied on Roman Numerals, which were cumbersome when it came to calculation. Even though the Arabic numerals appeared in Liber Abaci in 1202, it took another 400 years until they became ubiquitous throughout Europe, when the invention of the printing press aided in its widespread adoption.

Approach:

This problem is fairly straightforward. The description already tells you how to calculate the Fibonnaci numbers, and simply asks you to find the sum of the even valued terms which are less than four million. With some time and effort, you could easily do the problem by hand, although there is more educational value beyond simple addition (and efficiency!) if you solve it with a computer program. When I start out on these problems, I first create a mental outline of the solution, typically starting with brute force, and if I realize that a brute force solution would take too long, I try to come up with an indirect approach that may be more efficient. In this case the problem is simple, so I decided to use brute force. Here are steps in my mental outline:

  1. Generate the sequence of all Fibonacci numbers that are less than 4,000,000.
  2. Determine which numbers of the sequence are even numbers, then extract this subset.
  3. Add the subset of these even numbers. This will be the solution.

Solution 1:

For this solution, I first created a vector x containing the first two seed values, 1 and 2. This vector will be used to store the sequence of Fibonnaci numbers under 4 million. Next, I declared variables k and i, starting at 3 to be used as indices in the while loop that is used to calculate the terms of the sequence. I used a while loop because I do not know (at the time of writing the solution) the number of terms that fall below 4 million. The while loop allows me to keep appending terms to the vector x so long as the terms are less than four million. Once the value of the next term exceeds four million, the program exits the loop and moves on to the next line after the loop.

Within the loop itself, you see the line x <- append(x,k). This tells the program to append the value of k=3 to the vector x, or in other words, to append the third term of the Fibonacci sequence. The next line, k = k + x[i-1], sets k equal to its current value plus the value of the second to last element of the vector x (denoted by i-1, since there are currently i elements of the vector x). In other words, set k = 5. Then i = i +1 tells the program to increment i by 1, or in other words, set i equal to 4, which will be used to index the vector x during the loop’s next iteration when there will be four elements in the vector x.

During the next iteration of the loop, k is now equal to 5, i is now equal to 4. Append k to x so that the sequence becomes (1,2,3,5). Then set k = 5+3 = 8. Then set i = 4+1 = 5. The loop continues until all the terms of the Fibonacci sequence under 4 million are contained in x.
The last line of the program tells the computer to take the sum of all the even elements of x. The index[x%%2==0] is a predicate telling the computer to extract the subset of x where 2 divides each element evenly. The %% operator is the modulo operator, which returns the remainder of x and 2. When the remainder is equal to 0, that means 2 divides x evenly. The sum over the subset returned is the answer, 4,613,732.

Solution 2:

In this solution, I was able to remove the variable i, by noticing that it was sufficient to calculate the next term of the Fibonacci sequence by adding the largest two terms of the vector x. This calculation is represented by the line k = k + max(x[x<k]).

Solution 3:

Here, I was able to shorten the solution to five lines by removing the variable k. Here, I tell the the program to simply append to x, the sum of the current largest two values of x. This calculation is represented by the line x <- append(x,max(x)+max(x[x<max(x)])).

Posted in: Logs, Mathematics / Tagged: , , , , ,