Author Archives: Gene Dan

No. 96: Project Euler #22 – Three Solutions

14 August, 2013 9:18 PM / Leave a Comment /

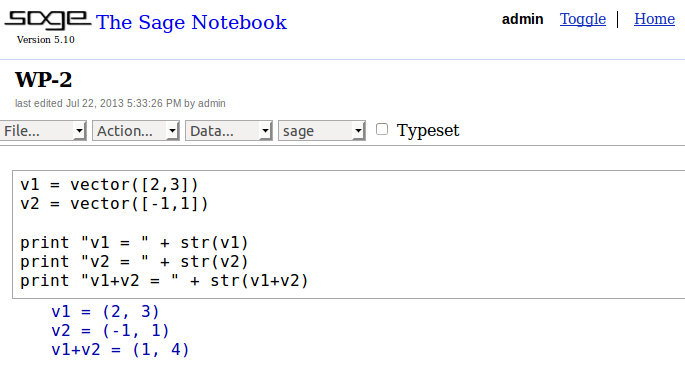
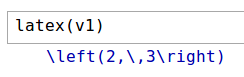
I’ve been using R a lot more at work lately, so I have decided to switch languages from VBA to R for my attempts at Project Euler problems. As of today I’ve solved 25 problems, 8 in the last day. I’ve found that R is much more powerful than VBA, especially with respect to handling vectors and arrays via indexing.

Here is the problem as stated:

Using names.txt, (right click and ‘Save Link/Target As…’), a 46K text file containing over five-thousand first names, begin by sorting it into alphabetical order. Then working out the alphabetical value for each name, multiply this value by its alphabetical position in the list to obtain a name score.

For example, when the list is sorted into alphabetical order, COLIN, which is worth 3 + 15 + 12 + 9 + 14 = 53, is the 938th name in the list. So, COLIN would obtain a score of 938 × 53 = 49714.

What is the total of all the name scores in the file?

The problem asks you to download a file containing a very long list of names, sort the names, and then assign each of the names a score based on their character composition and rank within the list. You are then asked to take the sum of all the scores.

The problem requires you to manipulate a long list of names.

The problem requires you to manipulate a long list of names.

Solution 1

My first solution consists of 15 lines. First, I imported the text file via read.csv() and assigned the sorted values to a vector called names.sorted. I then ran a loop iterating over each of the names, applying the following procedure to each one:

  1. Split the name into a vector of characters
  2. Use the built-in dataset LETTERS which is already indexed from 1-26 to assign a numeric score to each letter that appears in the name. The which function is used to match the characters of each name to the index (the value of which is the same as the score) at which it appears in the dataset LETTERS.
  3. Sum the scores assigned to each letter, and then multiply the sum by the name’s numeric rank in names.sorted. Then append this value to a vector y.

After the loop, the function sum(y) takes the sum of all the values in the vector y, which is the answer to the question.
Here’s the code for the first solution:

Solution 2

After solving the problem, I decided to write an alternative solution that would reduce the number of variables declared. I used the function sapply to apply a single function over the entire vector names.score:

This method allowed me to remove one of the loops and to remove the variables names.v, y and z.  This reduced the number of lines of code from 15 to 6.

Solution 3

I then found out I could further reduce the solution to just 2 lines of code by using nested sapply() functions over the names variable:

Here, I got rid of the names.score variable and only declared a single variable. The nested sapply() functions are used to first iterate over each element of the vector names, and second, to iterate over each character within those elements of the vector. The sum() function is wrapped around the nested sapply() functions which produces the solution by summing the scores of the individual names.

As you can see, R comes with some neat features that great for condensing your code. However, there are some tradeoffs as the first solution is very easy to read, whereas the last solution may be difficult for people to read, especially if they are not familiar with R. Loops are quite easy to spot in most widely used languages, so someone who knows C++ but not R should be able to read it. In order to understand the last solution, they may have to look up what the sapply() function does. Personally my favorite is the second solution, which I think has a good balance between being compact and being easy to comprehend.

Posted in: Uncategorized / Tagged: , ,

No. 95: My Thoughts on Computer Literacy

12 August, 2013 9:12 PM / Leave a Comment /

Last week, I ran across an article on Hacker News. It was written by a school teacher who bemoaned the lack of computer literacy amongst today’s youth. The basic idea is that despite the stereotype that kids these days are a bunch of tech-savvy computer wizards, it is actually the case that the opposite is true – kids can’t really use computers. The author contends that the increasing ease of use of computers, along with the increase in the consumption of entertainment media amongst today’s youths has brought about a corresponding decline in their ability to understand how computers work, and how to use them to solve problems.

I personally thought the blog post was one of the best pieces of news I had read all week, but based on the comments I’ve seen it looks like many people thought otherwise. Most of the posters on Reddit thought the author was a stereotypical, arrogant IT nerd, whereas most of the users on Hacker News were more supportive. In the midst of the author’s bitter ranting, I think many of the readers overlooked what I thought was the most important piece of his article:

Tomorrow’s politicians, civil servants, police officers, teachers, journalists and CEOs are being created today. These people don’t know how to use computers, yet they are going to be creating laws regarding computers, enforcing laws regarding computers, educating the youth about computers, reporting in the media about computers and lobbying politicians about computers.

I think the main flaw of the article is that the author spent too much time ranting about people’s struggles with basic troubleshooting and not enough time expanding on technological illiteracy’s greater impact on society regarding the freedom of speech, censorship, and governmental control. Nevertheless, I encourage anyone who is interested to read the whole thing.

My Thoughts

1. Breaking Stuff

When I was growing up, I was lucky enough to have access to computers at a time when they cost $10k per unit. However, as a child, I never put much thought into what computers could do other than to serve as a station on which I could play video games. I had a vague idea that they could be used for more important things, but I didn’t have any understanding as to what those things were. All I knew was that Dad would leave for work at 5:00 AM in the morning, do things on a computer he used at work and then return home, and as a result of that activity we were able to afford things like food and shelter. What I do remember is that like most kids, I would mess around with stuff at home and computers were no different – I would fiddle around with the settings and configurations, install random software and so on and so forth, which often led to things like system failures, viruses, and so on and so forth. As a result, my Dad would get angry (understandably), spend many hours restoring the machine to its pristine state, and give me a stern warning not to screw it up again.

That tone continued throughout high school and college – my parents provided me with most of what I needed, using their hard-earned money to pay for it. As a result, I was discouraged from experimenting with our possessions (as experimentation usually led to breakage). After college, I started having an interest in computers, and when I became financially independent, one of the first things I did was buy a whole bunch of computer parts and put together a machine by myself. Overall, the process was pretty easy, but I did make some mistakes on my first try – I accidentally destroyed my CPU and broke off some parts of my original motherboard, resulting in me spending hundreds of dollars replacing the parts. However, through these mistakes I became better at assembling computers, and became more careful while handling the parts. Furthermore, since I had my own financial stake in the equipment, I paid more attention to maintenance and I put more effort into repairing things when they stopped working.

I think kids should be encouraged to mess around with their possessions, on the condition that they learn how to repair them if they accidentally break them. This approach requires a bit more financial investment as parts need to be replaced if all options of repair have been exhausted. Because of this, replacement should only be done if it’s an absolute necessity – otherwise if kids knew they’d get everything they break replaced, they wouldn’t try as hard to fix the things they already have. I believe that breaking things – and subsequently repairing things – teaches people the limits of what their possessions can and can’t do, and under appropriate constraints, gives them more control, knowledge, and appreciation of their belongings.

2. The Spread of Ideas

The internet is a wonderful thing. The internet has give us access to information that we would have otherwise had to either spend lots of money, travel great distances, or wait for extraordinarily long periods of time to obtain. The internet has not only greatly reduced the cost of knowledge but also the cost of communication – it is no longer necessary for people of similar interests to meet in a single physical location to share their ideas. For instance, suppose you were an expert in a particular area of mathematics working on a problem that perhaps only you and five other people could understand. Without the internet, you might have never known about these other people’s existence, but now the internet has allowed experts to collaborate with each other and solve problems.

When I was growing up, I was interested in a number of subjects that I simply did not have access to. The local library’s selection was sparse and didn’t contain the appropriate volumes for my reading level. Now that internet use has become ubiquitous, I can find much of the information I want for free, and if I wanted to obtain a copy of a book on an academic subject such as Topology, Analysis, or Computer Science, I can choose from pretty much any book that’s currently in print. Rare books – such as George Carr’s Formulas and Theorems in Pure Mathematics and even the Voynich Manuscript (of which there is only one original copy), are available for free.

What this means is that the internet, driven by computers, not only allows people to acquire knowledge, share ideas, and solve problems incredibly quickly, but also increases opportunity for the common person. For instance, If I wanted to find someone who could build me specialized equipment for an experiment, I could do it pretty easily via the internet – this allows the builder to find a customer who’s willing to pay for his services, and for me to obtain the equipment I need. Easy access to communication makes both parties better off.

3. On Censorship, Freedom of Speech, and Control

Our ability to communicate not only dictates how we are able to share ideas, but also our ability to think. In our society, we are electing officials who will enact laws governing our nation’s telecommunications infrastructure. The level of technological literacy amongst the population not only directly affects the pool of competent candidates from which to choose from, but also our ability to determine which candidates are technologically competent enough to make decisions regarding what we can and cannot do with our computers.

There are many dimensions to this problem. First, a low level of technological literacy means that knowledge – and hence power – resides within the hands of a few people. Concentrated knowledge allows the people who hold this knowledge to take advantage of those who are ignorant. People who are not aware of how far technology permeates society aren’t thinking about how technology can be used to control our thoughts and our actions, or how it could be used to imprison people and deny them a right to a fair trial. Second, a low level of technological literacy means that society cannot accurately judge a leader’s competence regarding technical matters. We could very well, through complete ignorance, elect a leader who cannot make the right decisions when it comes to enacting laws. Third, technological illiteracy hinders our ability to prioritize how we invest our resources into our economy and society. For the reasons stated in (2), a fast and reliable communications network improves the knowledge base of the populace and allows them to take action to better their own lives through the sharing of ideas, along with the exchange of physical goods and services.

And finally, on censorship. Humans communicate with each other via mutually intelligible signals, such as language. Language allows people to transmit ideas across physical distances, and with the aid of encryption, they are able to do so very securely without the fear of interception. The freedom of thought and speech is critical to our survival – it allows us to comprehend how an authority figure might be abusing its power – and when such abuses are discovered, it allows the discoverer to transmit information about such abuses across a communications network and from there on the information will be acquired and digested by the populace. Access to such information, granted through the freedom of communication allows people to collaborate, take action against such abuses and hence improve their own circumstances.

So why does technological literacy play such a crucial role with respect to the freedom of speech? Most people would regard the freedom of speech as being important but they aren’t thinking hard about why they ought to learn about technology in order to defend it. Technological literacy allows us not only understand what technology can and cannot do, but also gives us a realistic picture of the current challenges we face when it comes to things like cybersecurity and regulation. There is a lot of fear being propagated by the media on cyber attacks, malware, hackers, and so on and so forth – and such fear is often used as an excuse to enact laws that curtail our freedom. Censorship forbids us to transmit certain types of information – and hence certain types of thought across cyberspace. It restricts access to information and the sharing of ideas, and from there the sharing of goods and services, along with the ability for people to collaborate with one another for their own good. With censorship, social progress comes to a halt. It is therefore to our benefit that we promote literacy amongst the population to enable ourselves to take action against what we see as unjust, and to protect our freedom to better our own lives.

Posted in: Logs

No. 94: Moonwalking with Einstein

5 August, 2013 9:27 PM / Leave a Comment /

Yesterday, I read a book called Moonwalking with Einstein, by Josh Foer. It’s a short tale about a journalist’s progression from being an absolute beginner at memory sport to winning the U.S. championships within a year. I’d first heard of Foer a couple years ago after reading an article about him in the NYTimes (the article is very similar to what happens in the book, so if you’re interested I recommend that you read it). I subsequently heard about his book a year later, and I finally got around to reading it last weekend. This is the first time I’ve ever read a book of this length (326 pages) in a day – I’ve been working on my reading speed over the past year and I think getting through this book has shown that practice has paid off (I still read a lot slower than some of my friends, who are super fast).

The sport of memory consists of  a bunch of tournaments where contestants undergo a series of competitions – memorizing lines of poetry, faces, decks of cards etc. The current world record for memorizing an entire deck of cards is 21 seconds….However, despite these seemingly inhuman feats, the competitors claim that the ability to memorize such things is within the grasp of the average person, and with enough practice it shouldn’t be too difficult to say, memorize a deck of cards within a minute. The book begins with Josh’s visit to the World Memory Championships as a spectator, where he interviews a few of the contestants for one of his assignments. During the interview, two of the competitors reckon that they can train Josh to win the United States championship – considered uncompetitive by international standards – with about an hour a day of practice. In addition to covering Josh’s preparation for the U.S. Championships, the book also has some interesting information about the role of memory in both ancient and modern education, along with its decline in recent centuries due to the proliferation of print media and the widespread availability of electronic storage.

Back in the day before the printing press was invented, scholars would have to travel great distances to get their hands on written texts, and when they actually had access to them, it often wasn’t for a very long time. Thus, early scholars had to rely on memory as their primary means of storing and retrieving factual knowledge. They would often memorize entire books during their stay at a library because when they got home, the only way to re-reference these texts was through mental recall (in fact, being able to recall the entire Aeneid was an unremarkable feat). However, the arrival of the printing press dramatically reduced the cost of storing and accessing information, and from then on the importance of memory declined.

Today, almost everyone in the developed world owns a mobile phone, and with it we have lost the need to remember phone numbers, dates, emails, and pretty much whatever factual information we can find through a quick search of Google or Wikipedia. Furthermore the emphasis on memory has declined in western education systems as educators have dismissed monotonous “drilling” as a mindless exercise, focusing more on relationships between concepts, or symbolic interaction amongst abstract ideas. My opinion is that the system has deemphasized memory to such an extreme that students no longer have the factual foundation from which to draw meaningful conclusions about their everyday lives and the society around them. It can definitely be harmful if rote learning is the only thing that a student learns, so while I am supportive of higher-level reasoning, I believe it must be built upon a solid foundation of factual knowledge.

You can make some pretty wacky arguments that are valid, but in our everyday world mean nonsense, for instance:

The Moon is made of blue cheese

Anything that is made out of blue cheese can recite the poetry of Homer

Therefore, the Moon can recite the poetry of Homer

The argument above is considered valid – assuming that the two propositions are true, the conclusion logically follows. However, despite this argument’s validity it doesn’t make any sense. The Moon isn’t actually made out of blue cheese and it can’t actually recite the poetry of Homer. Now consider the words we use in every day conversation. The words we use to form our own thoughts and to communicate with each other must simply be memorized if we are to accomplish these things with reasonable efficiency. We use words, along with facts, to form associations with what we know and to guide our thoughts and emotions. The fact that a sixth of Poland’s population died during World War 2 may seem meaningless if it’s some answer choice on a multiple-choice test, but when you come across this figure while reading a text on the subject, it makes you think. That’s a lot. That’s atrocious. It would be good if something like that didn’t happen ever again. It makes me feel sad that this occured. To assume that factual and conceptual learning are independent is naive, when in reality the two are closely entwined. Facts are important. They make us think and they make us feel – they are the foundation upon which we solve the world’s problems by way of logic.

Posted in: Logs / Tagged: , , ,

No. 93: On Ramanujan

29 July, 2013 8:52 PM / Leave a Comment /

I had first learned of Srinivasa Ramanujan during my junior year of college when I was flipping through the pages of my number theory book, reading the various biographies of the text’s featured mathematicians. I stumbled upon Atle Selberg’s profile, which mentioned that he was inspired to study mathematics after reading the work of Ramanujan, an early 20th-century Indian mathematician. From there, I read the remarkable story about Ramanujan’s upbringing, how he was born into poverty and, despite having no formal training in rigorous mathematics, produced some of the most profound results pertaining to number theory. I learned that although he was poor, Ramanujan benefited from his network of friends – a group of Brahmin intellectuals who recognized his mathematical talents and encouraged him to seek help by writing to three of the world’s leading mathematicians of the day – H.F. Baker, E.W. Hobson, and G.H. Hardy. While Baker and Hobson dismissed Ramanujan’s work, Hardy decided to bring Ramanujan to Cambridge and subsequently worked with him over the next six years, until his untimely death at the age of 32.

This wasn’t the first time I encountered Hardy’s work, I believe I first saw mention of his name when I was taking AP Biology in high school via the Hardy-Weinberg principle regarding the inter-generation distribution of genotypes in a population. We weren’t required to know the principle in detail – we just had to memorize some basic facts regarding what subject area it covered and why the principle was important. It wasn’t until I had read Hardy’s A Mathematician’s Apology 7 years later that I connected his name with what I had learned as a junior in biology class (although, I would imagine, based on Hardy’s writings that he would be disappointed to see his name connected to a practical application in biology).

Around the time I had been applying for jobs after college, I came across a book called The Man who Knew Infinity, which is a biography of both Ramanujan and Hardy, their respective upbringings, and their time collaborating with each other at Cambridge. I had placed it on my list of books that I would like to read and finally got around to it earlier this month during the 4th of July weekend and finished it earlier this morning. I’d say it’s my favorite biography – not only did it cover the lives of Ramanujan and Hardy, but it also covered the socioeconomic and political atmosphere during the early 20th century in both the British Raj and the British Isles.

What strikes me the most is that there were so many times in Ramanujan’s life where he was destined for failure – he failed out of college not only once but twice – not because he wasn’t smart enough to pass the examinations, but because he was so focused on mathematics at the time that he neglected his other subjects. There were numerous occasions where he nearly starved to death, and resources were always an issue – he had only a handful of books from which to extrapolate his discoveries, one of which being Loney’s Plane Trigonometry, and another being George Carr’s Synopsis of Pure Mathematics, a study guide for the mathematical Tripos examination at Cambridge. Hardy speculated that if it weren’t for his early death and haphazard upbringing, Ramanujan could have been the greatest mathematician who ever lived. It’s stories like these that are not only inspiring but also make you thankful for your circumstances. It makes you question whether or not you’re doing the best with what you’ve got or if you’re just throwing it all away.

Posted in: Logs, Mathematics / Tagged: , , , ,

No. 92: Vector Addition in SAGE

22 July, 2013 8:03 PM / 1 Comment /

Today I’d like to introduce you to some simple examples of vector addition in SAGE. I have been reading Lang’s introductory text to linear algebra, the first chapter of which covers properties of vectors.

SAGE can be used alongside Lang’s text as a gentle introduction to computer algebra systems. In my experience, I’ve found that bridging the gap between computer and paper mathematics can be intimidating, especially if a mathematics student doesn’t have a background in computer programming.

I’ve previously outlined why I think SAGE is an ideal educational tool, but to rehash it’s mainly because SAGE is open source and it uses Python as the language to execute commands. The open source nature of the software allows the student to examine what exactly is going on behind the user interface, and Python is a high-level programming language that lets the student execute commands right away without getting bogged down with low-level details like computer memory management.

To get started, I’ll declare and print two vectors in SAGE, v1 and v2:

wp_92-1

The first two lines in the above example declare the two vectors as variables, and the last three lines print v1, v2, and their sum in the output. Declaration of variables and the print function should be familiar to Python users.

We can also use SAGE to display the vectors in prettyprint, which means to display the vectors in a manner similar to what you’d see in a publication:

wp_92-2

Furthermore the latex() function outputs the LaTeX code – which is what you’d use to typeset such a publication:

wp_92-3In this case you would type \left(2,\,3\right) in your LaTeX editor.

In the following diagram, you can see that each vector can be represented as a point on a two-dimensional plane. v1 and v2 are represented in blue and red, respectively, and their sum, v1+v2, in purple:

[code language=”python”]
show(plot(v1,color=”blue”)+plot(v2,color=”red”)+plot(v1+v2,color=”purple”))
[/code]

wp_92-4

We can now use SAGE’s plotting capabilities to depict the Parallelogram Rule for vector addition, which states that the sum of two vectors can be represented as the fourth vertex of the parallelogram whose other three vertices are the two component vectors and the origin:

[code language=”python”]
l1=line([[1,4],[2,3]],linestyle=”–“,color=”black”)
l2=line([[-1,1],[1,4]],linestyle=”–“,color=”black”)
show(plot(v1,color=”blue”)+plot(v2,color=”red”)+plot(v1+v2,color=”purple”)+plot(l1)+plot(l2))
[/code]

wp_92-5Here, I have declared two additional variables as dashed line segments, and added them to the plot to complete the parallelogram.

SAGE also lets you declare and plot polygons. In the example below I have declared two polygons, p1 and p2, and shaded them in violet blue and violet red, respectively:

[code language=”python”]
p1 = polygon([(0,0),(1,4),(2,3)],rgbcolor=(138/256,43/256,226/256))
p2 = polygon([(-1,1),(0,0),(1,4)],rgbcolor=(219/256,112/256,147/256))
show(plot(v1,color=”blue”)+plot(v2,color=”red”)+plot(v1+v2,color=”purple”)+plot(l1)+plot(l2)+plot(p1)+plot(p2))
[/code]

wp_92-6As you can see, the parallelogram can be depicted as two triangles of equal size.

That’s it for today. I’ll soon follow up with another post on vector multiplication, and maybe some more properties such as equivalence and parallelism.

Posted in: Logs, Mathematics / Tagged: , , , , , ,