Author Archives: Gene Dan

Hi everyone!

It’s been a very long time since I last updated and I have so much to write about – race reports, employment, learning math and computers, and so on and so forth, but I need to keep it short since I have to wake up early tomorrow morning. So, today I’ll be writing about a project that I’ve been working on – brute-force password cracking to help me learn more about permutations and combinations, recursion, efficiency, and possibly multithreading later on. Of course, the most important issue here is cybersecurity and how to prevent attacks.

Let me stress that cybersecurity awareness is an extremely important issue in our day and age and when you have your money, identity, and livelihood entrusted to computers, you need to know how people can access your information and how to reduce the likelihood of attacks or prevent them all together. So, I’m going to give a basic demonstration on one of the most basic methods of password cracking – brute force calculation.

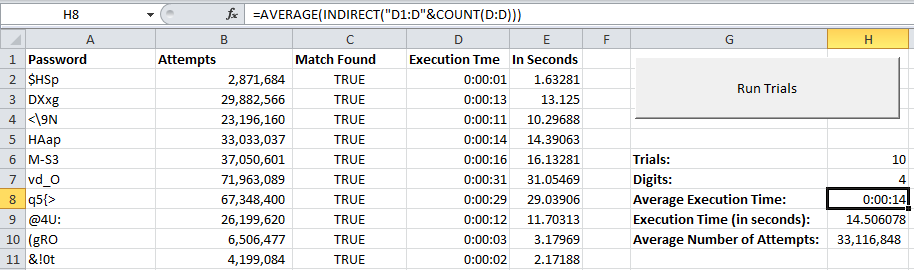
Brute-force cracking is a method by which the computer attempts to crack a password by using every possible combination of passwords until it finds a match. The time it takes to crack a password depends on the length of the password and the speed of the computer. The longer the password, the longer it takes to crack a password, and the more powerful the computer, the faster it can crack the password. The following picture shows how quickly a slow program that I wrote (in the computing world) – in Microsoft Excel – can crack a 4-digit password with a set of 94 printable ASCII characters (click to enlarge):

For 10 trials, it took Excel an average of 14 seconds to break each password.

As you can see, it took an average of 14 seconds for Excel to crack each password – and these aren’t your typical “dumb” passwords either. Combinations like “$HSp,” “DXxg,” and “<9N” extended out to 8 or more characters would be impossible for a human to guess and would be considered “good” by today’s standards. With brute-force calculation human creativity with respect to password creation doesn’t matter – since the computer checks all the combinations, theoretically, given enough time it will surely find with 100% probability, the password.

Luckily, the most powerful tool we humans have against this sort of attack is password length. From a library of 94 printable ASCII characters, each additional character in a password will make the computer work 94 times longer. For instance, it took about 0.005 seconds to crack a password of length 1, 0.07 seconds to crack a password of length 2, 1 second to crack a password of length 3, 14 seconds for 4, 196 seconds for 5, and so on:

The time it takes for Excel to find a match exhibits exponential growth.

As you can see, a password of length 12 will take about 700 years for my computer to solve, not including the time it takes to simulate keystrokes and button clicks, navigate dialog boxes, and so on. The simple solution? Make your password long! A long password means most people will not bother to use this method given current technological constraints. Of course, this presents a much bigger problem when we’re talking about governments, who control supercomputers that are much, much faster than what we can buy in the store. In this case, simple passwords won’t cut it.

Now the exciting part! I know you are all dying to see the code, so here it is in all its glory. It’s remarkably simple, and only takes up about 65 lines of code in three modules. Here’s the first one:

[sourcecode]
Option Explicit

Sub test(compstring As String, pstring As String, places As Long, attempts As Double, matchfound As Range)

If matchfound = True Then Exit Sub

Dim x As Integer, breaker As String

For x = 33 To 126 ‘ASCII character codes 33 to 126
breaker = pstring & Chr(x)
If places > 1 Then Call test(compstring, breaker, places – 1, attempts, matchfound)
attempts = attempts + 1
If compstring = breaker Then
matchfound.Offset(0, -1).Value = attempts
matchfound.Value = "True"
Exit Sub
End If
Next x

End Sub
[/sourcecode]

This module is the heart of the program. What it does is it takes five arguments, the first of which is the original, randomly generated password. Of course in the real world we wouldn’t actually know the password, so this, and the code taking action upon the values passed by this variable, will probably deal with pressing the enter button and seeing if we gain access. Anyway, the second argument is the comparison string used to break the password. The third argument specifies the length of the comparison string, the fourth argument keeps track of the number of attempts, and the fifth argument is a range that refers to a boolean telling us if we’ve successfully reached our goal.

Now, in the real world we wouldn’t know the length of the password, so I had to create a procedure that would automatically increase the length of the comparison string if a match wasn’t found by the end of all the iterations for the current length. At first I tried using loops, but I found that it was much easier to conceptualize a recursive procedure than a looping procedure. I think loops tend to be more efficient, but recursive functions may be a lot easier to read and I think in this case it gives the reader a better understanding of what is going on. When the procedure runs out of combinations of a given length, it calls itself, incrementing the places argument by one to increment the length of the comparison string.

The other modules are higher level modules that control this procedure. They aren’t as exciting, but here’s the second one:

[sourcecode]

Sub main(anchor As Range, digits As Long)

Dim password As String, truthrange As Range
Dim m As Long, bdigits As Long
Dim exectime As Single
Dim exectime2 As Date

exectime = Timer
exectime2 = Now()
bdigits = 1
password = ""

For m = 1 To digits
password = password & Chr(WorksheetFunction.RandBetween(33, 126))
Next m

anchor.Value = "’" & password
Set truthrange = anchor.Offset(0, 2)
truthrange.Value = "False"

Do Until truthrange.Value = True
Call test(password, "", bdigits, 0, truthrange)
bdigits = bdigits + 1
Loop

anchor.Offset(0, 3).Value = Format(Now() – exectime2, "hh:mm:ss")
anchor.Offset(0, 4).Value = Format(Timer – exectime, "00.00000")

End Sub

[/sourcecode]

This module generates a random string which we designate as our password, feeds it into the first module and keeps track of the execution time. It also contains methods for printing the results on the screen. Here’s the third module:

[sourcecode]

Sub macromain()

Dim i As Integer, trials As Integer, digits As Long

Application.ScreenUpdating = False
Application.Calculation = xlCalculationManual

Intersect(Sheets("sheet1").UsedRange, Range("A2:E1048576")).ClearContents

trials = Range("TRIALS")
digits = Range("Digits")

For i = 2 To trials + 1
Call main(Range("A" & i), digits)
Next i

Application.ScreenUpdating = True
Application.Calculation = xlCalculationAutomatic

End Sub

[/sourcecode]

This third module takes user input found on the spreadsheet page indicating the desired number of trials and password length, and feeds this information into the second module. Right now it runs pretty slow and is only programmed to run on one core. My computer at home has three cores and if I can get them to calculate combinations starting from different places in the ranges of ASCII character codes (different places in the range 33 to 126), I can get it to run three times as fast, in my opinion. But that will be for the distant future. One of the more immediate goals I can achieve is GUI programming with keyboard stroke and button clicking simulation to emulate how a human navigates password dialog and text boxes.

And that’s it! What lesson did we learn here?

1) Make your passwords long!
2) For administrators, lock users out if they cannot correctly type in the password after 3-5 attempts. This will prevent the computer from trying the millions of combinations necessary.
3) Check your login data to see if anything looks unusual! If you see a login at a time you did not log in, someone may have taken your data.
4) Always, always use different passwords for different accounts, and don’t reuse your passwords. This will require the thugs to run a new brute force for every account, or find another solution elsewhere.
5) If you have time, spend it on learning how to secure your information. You won’t regret it!

Thanks for reading!

Hey everyone,

Today I thought of a small coding exercise for me to do to work on algorithm building – I decided to write a program that converts positive decimal numbers to binary numbers. I knew that I could probably find plenty of examples on the web of this algorithm, but I decided to find out for myself how the conversion worked before looking for any help. Anyhow, one method of algorithm discovery involves the application of that algorithm to a specific example known to be true, and then using that example to pick apart the steps. What I mean is that many of us use algorithms every day in order to solve problems without realizing it or understanding it. For instance, most of you have probably used the division algorithm daily ever since you learned it in kindergarten – for instance, to divide 7 by 2 we subtract the product of 3 and 2 from 7 to obtain the remainder 1. Thus, 7 divided by 2 equals 3 remainder 1. However, how do we know that this algorithm works every single time for every pair of integers? Fortunately prior math enthusiasts have given us a logically rigorous explanation. Looks more complicated when printed, right?

Now, let’s examine how to find the binary value of the integer 27. First, let me give a brief description on how binary values work. In the binary system, every digit of a number is represented by either 1 or 0, in contrast to our common base-10 system, or decimal system, in which each digit may be represented by 0,1,2,3,4,5,6,7,8, or 9. For instance 1 in base-10 is 1 in base-2, 2 in base-10 is 2 in base-2, 3 in base-10 is 11 in base-2, 4 in base-10 is 100 in base-2, and so on, and so forth. In base-2, 10 is twice as much as 1, 100 is twice as much as 10, 1000 is twice as much as 100, and in this manner each digit represents a unit that is twice as large as the digit to the right of it. Check out the link on the binary system to learn more.

Let’s go back to 27. You could try counting in binary (1, 10, 11, 100, 101, …) but that would take too long and would be cumbersome to program. An alternative method we could try is to break up the number 27 into different binary unit values (1000’s, 100’s, 10’s, 1’s), add them up and obtain the final binary representation. However, how many digits would the resulting binary number be? We can’t deduce the answer simply by staring at 27, so let’s try to divide by 2 and see what happens. After dividing 27 by 2, we get 13 remainder 1. What happens if we divide 13 by 2? We get 6 remainder 1. Dividing 6 by 2 gives us 3, and dividing 3 by 2 gives us 1 remainder 1. Note that we applied the division algorithm 4 times. It just so happens that 2^4 = 16, and that 10^4 = 10000. We know that 10000 in binary is equal to 16 in decimal because 10 in binary is equal to 2 in decimal and 10x10x10x10 in binary is equal to 2x2x2x2 in decimal. Thus, we know that 16 out of our original 27 consists of 10000 in binary. What about the other 27 – 16 = 11? We then take 11 and divide that by 2 to obtain 5 remainder 1, divide 5 by 2 to obtain 2 remainder 1, and divide by 2 to obtain 1. In this next round of divisions we have applied division by 2, 3 times. Thus 10x10x10 = 1000 in binary, which is equal to 8 in decimal. Now we have 11-8 = 3 remaining to consider. We divide 3 by 2 to obtain 1 remainder 1. We have applied division by 2 once, so 10 in binary is equal to 2 in decimal. Now we only have 3-2 = 1 remaining and 1 in decimal is equal to 1 in binary. So, we know that 16 + 8 + 2 + 1 in decimal is equal to 10000 + 1000 + 10 + 1 = 11011 in binary…success!

I must stress that this does not prove that the algorithm works – it has only worked in this one particular instance. However, this instance has shed some light, at least for now until I actually gain the knowledge to do a mathematically rigorous proof – which won’t be coming in a long time!

Using this example as a guide I wrote down some code:

[sourcecode language=”css”]
//Decimal to Binary Conversion

#include <iostream>
#include <cmath>
using namespace std;

const int base = 2;
long long baseconv(long);

int main()
{
long long inputval;

cout << "Enter an integer: _b";
cin >> inputval;
cout << inputval << " is " << baseconv(inputval) << " in binary!" << endl;
return 0;
}

long long baseconv(long input)
{
long long baseconv;
long long updater;
long long dival;
long digitcount;
baseconv = 0;

while (input > base – 1)
{
digitcount = 0;
dival = input;
while (dival > base – 1)
{
dival = dival / 2;
digitcount = digitcount + 1;
}
updater = pow(base, digitcount);
baseconv = baseconv + (pow(10,digitcount));
input = input – updater;
}
baseconv = baseconv + input;
return baseconv;
}

[/sourcecode]

Here’s an example of the output:

I’m running out of time so I don’t want to go into every single detail over this program, but in a nutshell, the program splits the input integer into separate binary parts, then adds the binary parts together in order to obtain the result. Unfortunately, the memory limitations of c++ do not allow me to convert very large integers, such as 1234123412341234. See what happens when I try to convert this value:

Also, the program does not work with negative values, so those will be two things that I will work on in the near future. I also spent the time to port the program into VBA, and I changed it to do conversions from base-10 to any base the user chooses:

[sourcecode language=”css”]
Function BASECONV(inputval As Long, base As Integer) As Variant

Dim dival As Long
Dim digitcount As Integer
Dim updater As Long

BASECONV = 0

Do While (inputval > base – 1)
digitcount = 0
dival = inputval
Do While (dival > base – 1)
dival = dival base
digitcount = digitcount + 1
Loop
updater = base ^ digitcount
BASECONV = BASECONV + (10 ^ digitcount)
inputval = inputval – updater
Loop

BASECONV = BASECONV + inputval

End Function
[/sourcecode]

Notice how much more efficient the code is! That’s because VBA is at a much higher level than C++, so there are a lot more built-in functions that do the work for you. Here’s an example of the output:

Hey everyone,

It’s been a while since I’ve updated so I’ll write a new post summarizing what’s been happening over the past few months. First of all, my Facebook account has been disabled since they’ve accused me of using a fake name. Of course, I have done no such thing and am upset and frustrated since I have a lot of pictures on there that I would have liked to keep for myself. Due to the enormous size of Facebook I’ll probably never see what I had on my page again and I don’t know if I would want to use a service that cannot accurately distinguish real accounts from fake ones. On the bright side, now that my account’s gone I’ll probably have more time to do something productive since Facebook is hardly the place to do that. I also wrote a lengthy blog entry detailing my experience at the Memorial Park Criterium, but after uploading my photos, WordPress crashed on me and all my drafts were lost. So remember folks, save your data often or else you will regret it!

Anyway, over the last few months I’ve been traveling all across Texas looking for work and racing bicycles. Fortunately, I had some success as I placed well in my remaining races (3rd at Chappell Hill, 7th at State Championships), but more on that later in other blog posts. I also landed a job so now that I’ve become employed I’ve had to rearrange my priorities and projects to suit my career. And some more good news – I achieved a perfect score on my second actuarial exam, FM/2! I had studied very hard the month before I took the test, but not so hard the month before that. I’m just glad that I probably got every single question right on that exam. I was pretty cautious during the test and took my time, using the entire three hours I was allotted for that exam. I didn’t feel entirely prepared but in retrospect I probably studied more than most people do for that test, since I read the entire textbook in the syllabus and did every single problem in the book – twice. Unfortunately my main goal was to read the text twice, but I felt so lazy for only reading it once, go figure! Perhaps I’m too cautious – given that there are an infinite number of possible questions – you can never be fully prepared!

I had to put Python aside and I probably won’t be able to go back to it until maybe the summer of 2011.  Fortunately, I’m learning two other programming languages in its place, C++, and VBA (Visual Basic for Applications), so the time I spent on python has definitely not gone to waste. C++ is harder, and I would have liked to learn Python first but I’ll have to make do since that’s what we use at work. I also finished a computer science textbook, a textbook on Microsoft Excel, and another introductory textbook on C++, as well as a couple of legal documents regarding my work. I’m currently reading my second textbook on C++,  and a textbook on VBA as well. Check out the projects page for more details.

Hey everyone,

Today’s problem actually consists of a potentially infinite number of problems! I’ve been learning some programming in my spare time, so I’ve written my first program using Python, a powerful high-level scripting language that can do several things. My first program is called “Gene’s Multiplication Tutor.” It simply picks random numbers for the user to multiply, lets the user pick the number of problems the user wants to do, and tells the user how many problems the user answered correctly. To download the program, click the following link:

Gene’s Multiplication Tutor

The link will take you to a page that hosts the file. Click “Click here to start download..” and save it to the desired directory. After you have the file, you will need to open up a command prompt or terminal window, cd to the directory at which the file is located, and type in:

python mult3.py

at the prompt to start the program. Of course, you will need a python interpreter in order to run the program. The program will first ask you if you wish to proceed, and if you wish to proceed, it will ask you how many problems you wish to do. After inputing the number of problems you wish to do, the program will ask you the questions, and will tell you whether or not you got them right after each answer. After all the questions have been answered, the program will tell you how many you answered correctly, and then will return to the menu.

Here are some screenshots:

Access the program through the terminal window.

It looks like I missed one. Bummer!

Enjoy!