Category Archives: Mathematics

No. 122: 25 Days of Network Theory – Day 5 – Visualizing Networks with D3.js

9 July, 2017 10:12 PM / Leave a Comment /

Today marks a milestone in my blog in the sense that I’ll be using D3.js for the first time. I’ve been interested in this library for some years now and I’ve finally gotten around to incorporating some simple examples into my blog.

D3.js is a JavaScript library for producing stunning visualizations – you may have seen several of them in Internet media publications and you can see some more examples on the D3.js homepage.

I think you can’t just be good with code to maser D3, you have to be a bit of an artist, because even if you understand the library well, your visualizations will look bad if you aren’t good with color coordination and web design.

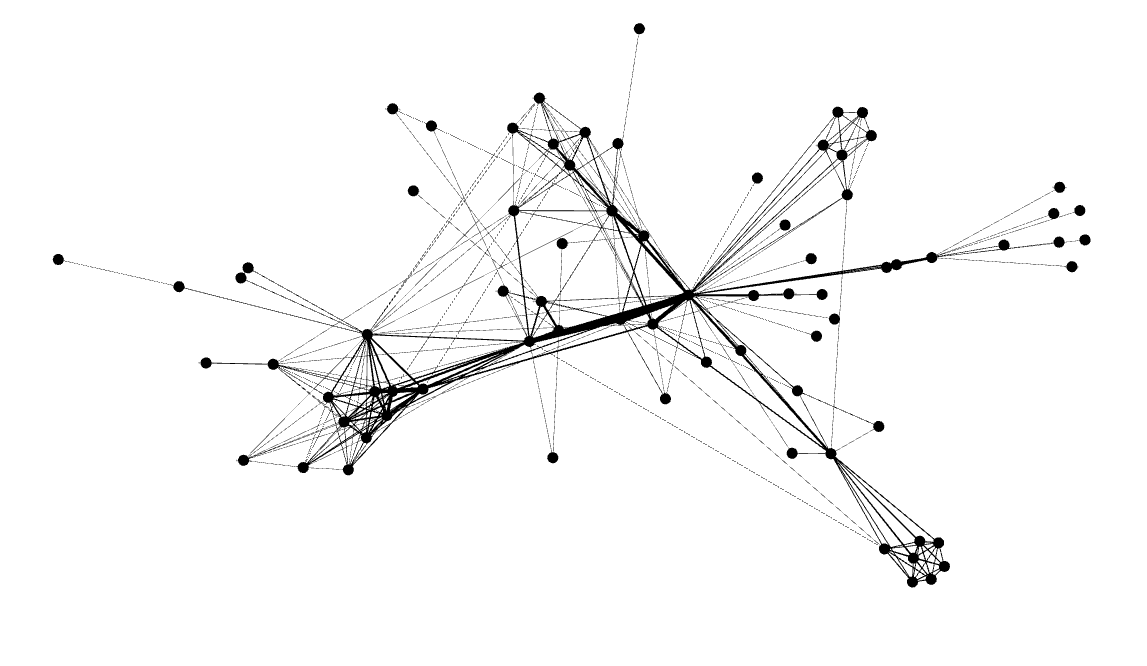
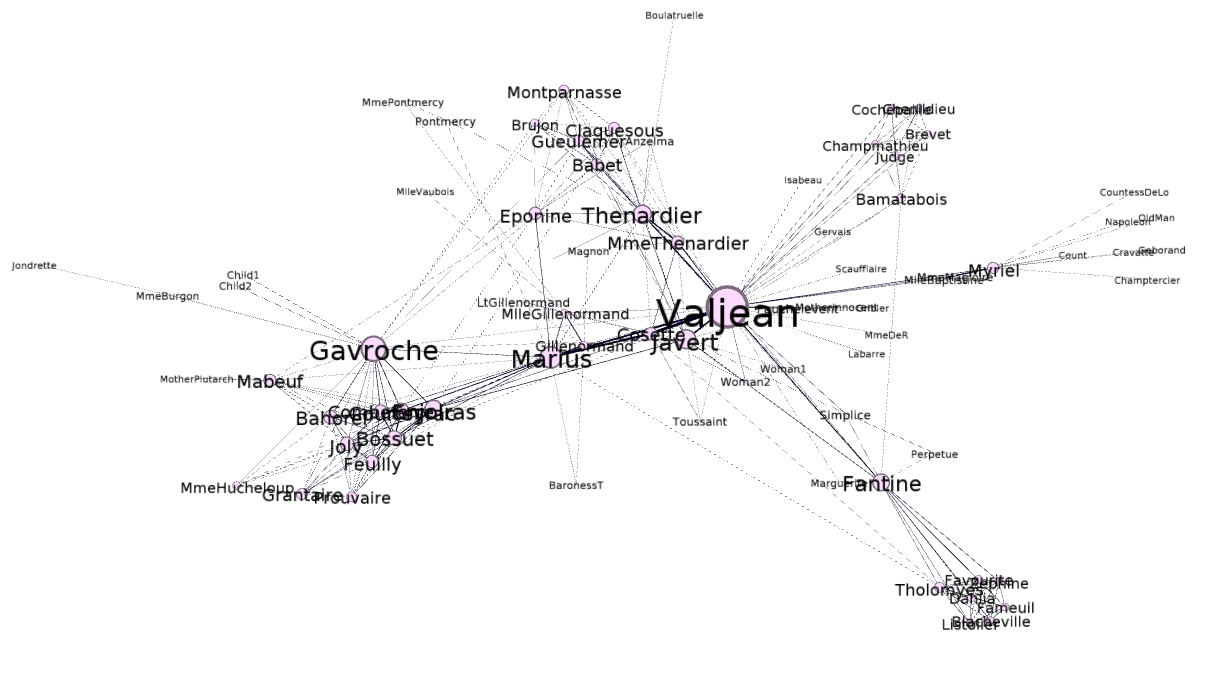
It turns out one of the core developers of the library had already done what I had set out to do today – create a D3.js graph using the Les Miserables data set:

You can see here that this visualization differs from the previous ones in that it’s interactive and dynamic – the nodes appear to be suspended in some kind of invisible goop and the edges are elastic. You can click on the nodes and drag them around and watch them snap back into place when you release them.

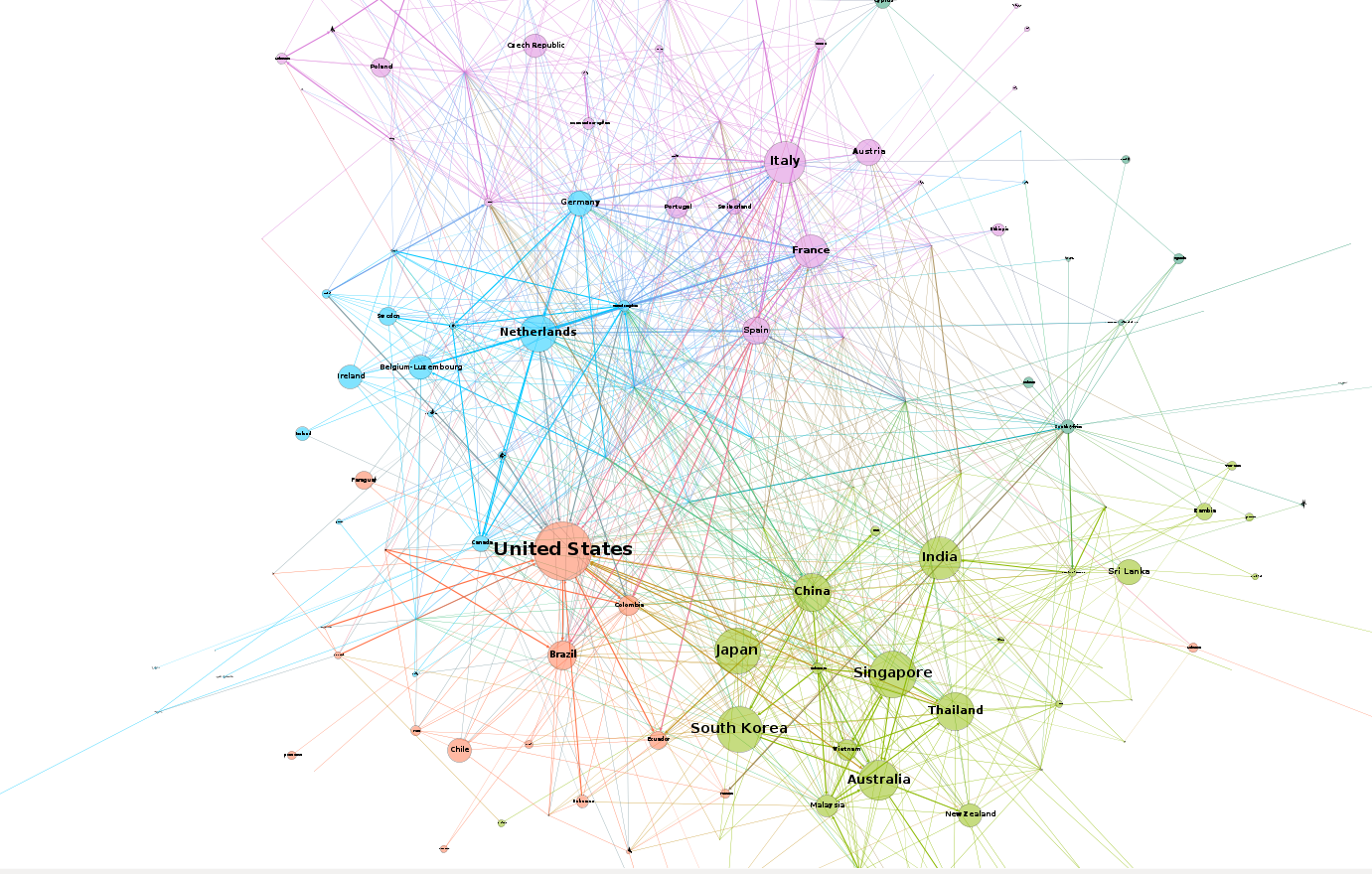
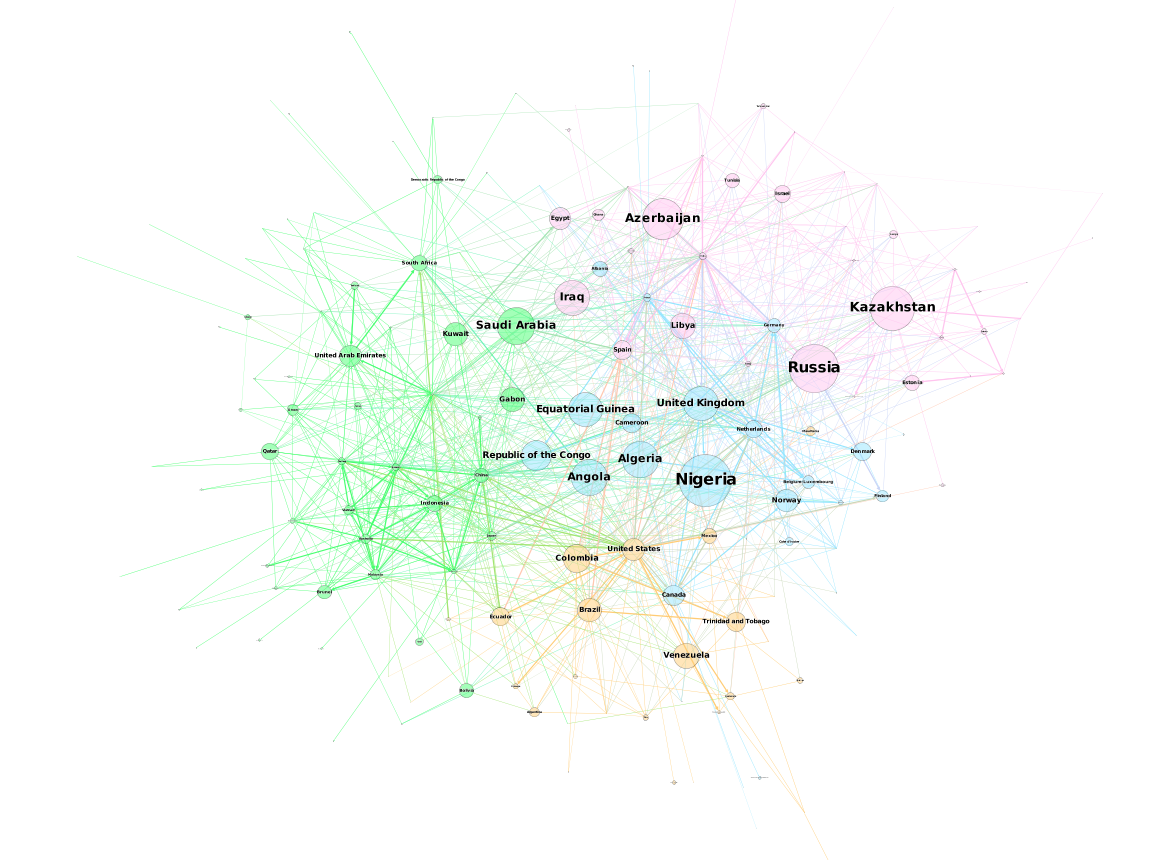
Since there’s no point in duplicating what has already been done, I’ve decided to adapt this template to the previous post’s data set, the international petroleum trade:

Compared to the Les Miserables visualization, this one appears to have a bit more inertia as the whole graph doesn’t move as much if you try to click and drag one of the nodes.

I didn’t have to do too much work – the hard part was just figuring out how to get the json format correct and consistent with the html file. I exported the modularity class from gephi into R and used that to color the nodes. R was used to create the json file:

Okay, so I guess there wasn’t much to add as far as theory goes. But I do think these visualizations are pretty cool, and add a level of engagement and interaction with the user that you don’t get with still images.

Posted in: Mathematics

No. 121: 25 Days of Network Theory – Day 4 – International Petroleum Trade

8 July, 2017 12:41 AM / 1 Comment /

As far as readings go, there wasn’t much to include from the text in today’s post since I just went through a section that covered some basic proof techniques (induction, contradiction, etc.). Tomorrow will be somewhat similar since that section covers general data gathering and manipulation. So today I’ll go over some data I stumbled upon while looking for other texts on graph theory.

The Observatory of Economic Complexity
MIT has some neat data sets here – these contain aggregate trading data for various commodities dating back to 1962. I was interested in looking at crude petroleum movements between countries in the most recent year available, 2014.

Creating a gexf file
Here’s the script I used to generate the gexf file that I imported into gephi. This is pretty much self-contained, and ought to run on your computer as is as long as you have the sqldf package installed. One improvement over previous code is that it fetches the datasets automatically, rather than having me point it out somewhere in my post. I also discovered a useful function called basename() which extracts the file name part of a url string containing a filename.

Generating the graph

After importing the gexf file, adjusting the graph for eigenvector centrality, and applying some community detection, gephi produced the following result:

Selection_275

Try clicking on the graph – you can zoom in quite a bit to see the countries and edges in detail. I’ve set the graph so that edge width is proportional to the log of the export value, so the higher the trading volume between two countries, the thicker the edge. We can also see that communities are highlighted in the same color – we would intuitively associate these with trading blocs, or groups of countries that work closely together.

In this graph, the node size is proportional to eigenvector centrality. In other words, the larger the node, the more important the country is to the network. To me, this was kind of puzzling. At least in my mind, I would have thought that major exporting nations like Saudi Arabia would have appeared much larger on the graph. However, you can see from the image that countries associated with importing oil dominate the graph.

I thought maybe it had to do with the direction of the edges. What we have here is a directed graph – if you look carefully you can see that the edges are actually arrows that point from the exporting country to the importing country. If we reverse the direction of these arrows – that is, recreate the graph from the perspective of money flowing into exporting countries rather than goods flowing out of those countries, we get the following graph:

Selection_274

This graph is a little more consistent with my intuition – we can see that major exporting nations like Saudi Arabia, Iraq, and Azerbaijan appear much larger, while importing nations appear smaller. However, I have to caution myself that just because the graph is consistent with my belief, doesn’t mean I’m right. I’ll have to see if I can further understand centrality as I continue in the course.

Posted in: Mathematics

No. 120: 25 Days of Network Theory – Day 3 – Edge and Vertex Connectivity

6 July, 2017 11:16 PM / Leave a Comment /

Oftentimes, we would like to think about the connectivity of a network, that is, how robust is a network to the removal of nodes and edges? I can think of several real-world applications where we might ask this question, for example:

  • Which roads can we remove from the transportation network such that people can still get to where they want to go?
  • Which metro stations would cause the most disruption to the network if they were destroyed?
  • What enemy bases should we target first if we want to disrupt their supply chain?
  • Where should we add roads, or other links between stations to increase the robustness of the network?
  • What would happen to a group of friends if certain people left? Would they still hang out?

…and so on.

This brings us to two measures of network cohesiveness – edge connectivity and vertex connectivity. Simply stated, edge connectivity measures the number of edges we would need to remove from a network in order to divide it into distinct components. For example, think about your daily commute. If we were to remove one of the roads on your commute, you would probably still be able to reach your destination, even though you’d have to find some other way to get to work. However, if we were to remove more and more roads, eventually you would be unable to get there, and at some point, if we remove even more roads, your workplace may become an inaccessible island separate from the rest of the transportation network. We would call your workplace a component, that is, a node unreachable from any other node. Edge connectivity measures the minimum number of edges we would have to remove in order to separate a network into distinct components. The higher the edge connectivity, the more edges we’d have to remove – so we can say that the higher this number, the more cohesive the network is.

Formally,
Suppose G=(V,E) is a simple network.

  • A disconnecting set of G is any subset S\subseteq E for which the network (V,E-S) has more components than G.
  • S is a cut-set of G if it contains no proper subsets that are disconnecting sets.
  • The edge connectivity of a network G=(V,E) is the number of edges in the smallest cut-set and is denoted by \lambda(G). If \lambda(G)\geq k then G is k–edge connected.

Formally, a set of nodes in a connected network is called a separating set if their removal (and the removal of incident edges) disconnects the graph. If the smallest such set has size k then the network is called k–connected and its connectivity, denoted \kappa(G), is k. If \kappa(G)=1 then a node whose removal disconnects the network is known as a cut-vertex.

Likewise, vertex connectivity measures the number of nodes we’d have to remove (along with their associated edges) in order to separate a network into distinct components. For example, consider the Hong Kong subway system:

hong-kong-MTR-system-map-1024x726

If you ever have the chance to ride the subway in Hong Kong, I recommend that you do – in my mind it’s the best subway system in the world. In network theory, we call this type of network a connected graph, that is, every subway station is reachable from every other station. If we were to remove Wong Tai Sin from the map, we’d still be able to reach every station from every other station. Likewise, we’d still be able to do so if we removed the stations on the periphery, like Chai Wan or Wu Kai Sha. However, if we were to remove just a single important station, say Quarry Bay, we would sever the eastern portion of the Island Line from the rest of the network. Thus, Quarry Bay is a cut-vertex of the Hong Kong subway system. Since vertex connectivity measures the minimum number of nodes we’d have to remove to separate a graph, we say that Hong Kong’s subway system has a vertex connectivity of 1. Like edge connectivity, the higher the vertex connectivity, the more robust the network.

Looking at our Les Miserables example, it’s pretty obvious that both the edge and vertex connectivity is one:

Selection_271

If we were to remove the edge between Myriel and Napoleon, we would separate the graph. Likewise, if we were to remove Myriel from the picture, we’d also separate the graph. This is a somewhat boring example, and output from the R console confirms this is true:

However, one neat thing the igraph package can do is determine the separating sets of minimum size that separate a network. The terminology is a bit different in the igraph documentation, but I was able to find a function that identifies what are called separators. It turns out there are several such separators in our example, and because the vertex connectivity of this network is 1, R returns 8 cut-vertices from the network:

There are some weaknesses to this approach. Just because the removal of a node disconnects a network doesn’t mean we shouldn’t remove such a node in a real world application. If node served as a connection to unimportant parts of a network it may be wise to remove it if the costs of maintaining such a node outweighed the benefits. I’m hoping that tools to address issues such as this will be introduced further along in the course.

Posted in: Mathematics

No. 119: 25 Days of Network Theory – Day 2 – Matrix Representations of Networks

5 July, 2017 7:39 PM / Leave a Comment /

Visualizations of networks can look pretty, but of course without a formal mathematical language to describe the properties of these networks, we will not be able to quantitatively answer the questions we would like to have answered about such networks. Today I’ll introduce two ways of defining networks in terms of matrices – adjacency matrices and incidence matrices, which connects the ideas of network theory with those of linear algebra.

Adjacency Matrices
Suppose G=(V,E) is a simple network where V={1,2,\ldots,n}.
For 1\leq i,j\leq n define

    \[a_{ij}=\left\{\begin{aligned} 1, & \quad (i,j)\in E, \\ 0, &\quad (i,j)\not\in E.\end{aligned}\right.\]

Then the square matrix A=(a_{ij}) is called the adjacency matrix of G.

Adjacency matrices are a way to define networks from the perspective of their nodes. The notation above simply specifies a square matrix whose rows and columns correspond to the nodes of the network. The each entry will be 1 if there is an edge connecting its corresponding row and column (which represent nodes) and 0 otherwise.

Going back to our Les Miserables example, the graph below:
Selection_266

Is represented by the following adjacency matrix:
Selection_267

Here, the column names are omitted, but they should follow the same order as the row names. If you add up the 1s in a row, the sum should be equal to the degree of the node that it represents. For example, the sum of the row that represents Jean Valjean (highlighted in the matrix above) equals 36. This is both consistent with the data from gephi and the theory represented in the text:

Selection_268

Furthermore, we can see that certain characters who are connected with Myriel have a degree of 1, such as Napoleon, Cravatte, and Champtercier, which are seen in both the matrix and the visual representation of the graph if we zoom in:
Selection_271

A short script was used to import the gexf data, convert it into an igraph object, and from there calculate and print the adjacency matrix.

Incidence Matrices

Suppose G = (V,E) is a network where V={1,2,\ldots,n} and E={e_1,e_2,\ldots,e_m} with e_i=(u_i,v_i).
For 1\leq i\leq m and 1\leq j \leq n define

    \[b_{ij}=\left\{\begin{aligned} 1, & \quad u_i=j, \\ 1, &\quad v_i = j, \\ 0 & \quad \text{otherwise.}\end{aligned}\right.\]

Then the rectangular matrix B=(b_{ij}) is called the incidence matrix of G.

Incidence matrices are a way to define networks from the perspective of edges. The notation above simply means that this time, we’ll have a matrix whose columns represent each edge in the network, and the rows represent nodes. Each entry will be a 1 if the character represented by a row participates in the edge represented by the column, and zero otherwise.

Unfortunately, igraph (at least to my knowledge) can’t calculate the incidence matrix for a nonbipartite graph, so I had to use a workaround I found on stackoverflow. I’ve also altered the in the definition from the original text to be consistent with this workaround (the original had a -1 for the v’s).

The LesMiserables network has 77 nodes and 254 edges, so we’ll have a very wide matrix that is too large to display on this webpage. However, I’ve added a screenshot to give just a glimpse as to what it looks like:
Selection_273
The code used to generate the matrix:

Posted in: Mathematics

No. 118: 25 Days of Network Theory – Day 1 – Introduction

5 July, 2017 11:14 AM / Leave a Comment /

Selection_265
I’ve decided to dedicate this month to the study of network theory. For the past few years, I’ve been intrigued not only by the theory’s simplicity – that a graph is simply a collection of nodes and edges, but also its ability to answer seemingly complex and qualitative questions regarding society (both human and nonhuman) in general, such as:

  • Who are the most influential members of society?
  • What are the most natural subdivisions for identifying communities within a population of people?
  • How can we construct a transportation system that optimizes traffic flow and minimizes traffic jams?
  • How can small disruptions spread through a network to cause financial crises?
  • How can we quantify consensus?
  • How are social norms and reputational effects enforced?
  • How quickly can a disease spread throughout a community?

…and so on.

At first glance, the above graph may not look like anything special – but there is indeed something very special about it. This network represents co-occurrences between characters in Victor Hugo’s Les Miserables. After we add some labels to identify the characters, and adjust the size of the nodes and labels to reflect the degree (that is, the number of edges a node participates in), the graph becomes more meaningful in that you can immediately identify the most important characters to the plot:

Selection_266

You can see that the largest node is represents Jean Valjean, the main protagonist of the story. This means that, at least according to degree, Jean Valjean is the most important person in the novel. However, there are several other quantitative measures of influence, and we will later see that Jean Valjean may not be the most influential character in the book, at least according to those other measures.

For this course, I’ll be reading Estrada and Knight’s, A First Course in Network Theory, and I’ll be reading 10 pages per day and applying what I learned there to the Les Miserables network.

There wasn’t much to the first ten pages other than to introduce the history of graph theory (there was a section on the Seven Bridges of Königsberg). So, I’ve used this opportunity to introduce what tools I’ll be using for the course of study. There’s gephi, a graph visualization program, igraph, a package that I’ll be using to perform more quantitative analyses on this network in R, and the Les Miserables network dataset itself.

Posted in: Mathematics