Section: 1.2 – Row Reduction and Echelon Forms
Status: On target
Today I’ll demonstrate a couple of algorithms performed on a 3×4 matrix (we’ll call it A) performed in SAGE. SAGE is an open source computer algebra system intended as an alternative to proprietary systems such as Mathematica, MATLAB, etc. I’ve written about SAGE a few times, here, here and here. To begin, we’ll define A as follows:
\[A=\left[\begin{array}{rrrr} 1 & -2 & 1 & 0 \\ 0 & 2 & -8 & 8 \\ -4 & 5 & 9 & -9 \end{array} \right] \]
To define this matrix in SAGE (actually I think a more modern name would just be “sage”), we can open up the Linux terminal and use Python commands to assign the matrix object to the variable A:
Those who are familiar with the Python programming language will know that the dir() function returns a list of methods that can act upon an object. Methods are functions that are defined within classes that can act upon instances of those classes. Here, we can use dir() to determine what methods are available to us through sage:
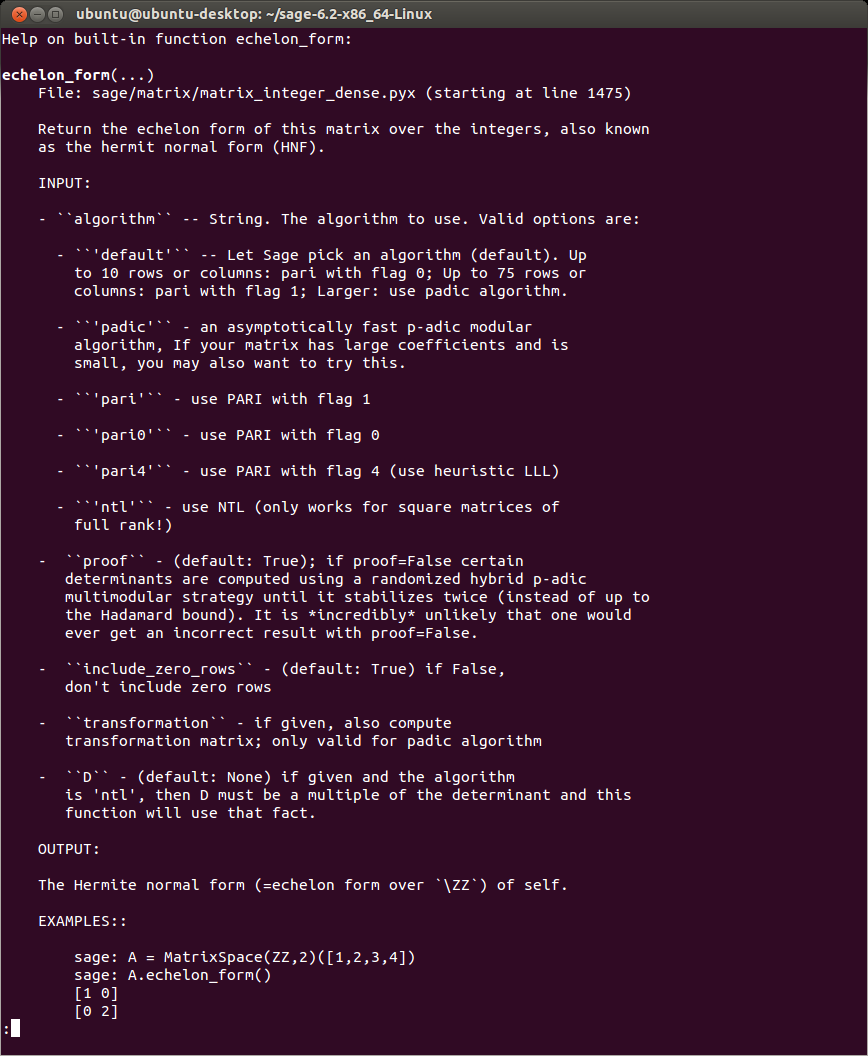
For new users, the variety of methods can be bewildering and somewhat intimidating – but if you look closely you’ll find a method called ‘echelon_form’, which is exactly what we’d guess – a function that returns the row echelon form of our matrix A. Before proceeding, we can type help(A.echelon_form) which confirms that the method does indeed perform the algorithm that most students learn within the first week of their Linear Algebra course (except much faster!):
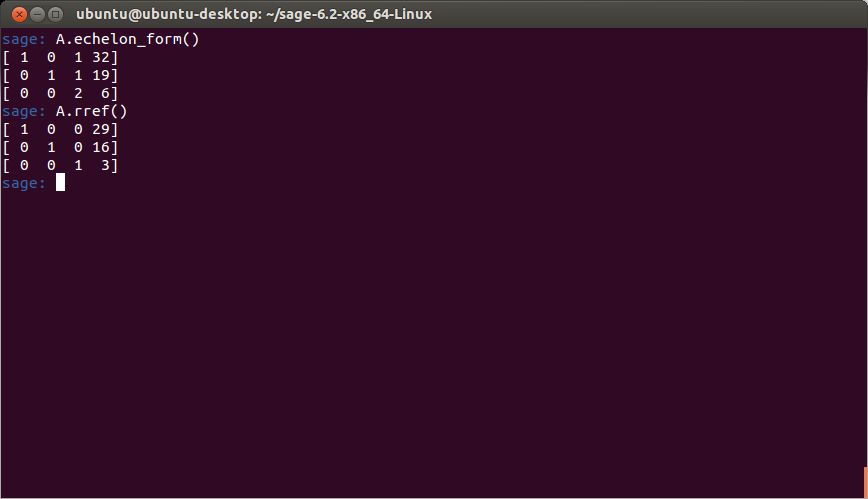
Now, typing in A.echelon_form() returns the echelon form of A. The method rref stands for reduced row echelon form, which produces the solution to A’s equivalent linear system:
As you can see, the solution is the point (29, 16, 3).