This entry is part of a series dedicated to MIES – a miniature insurance economic simulator. The source code for the project is available on GitHub.
Current Status
Last week, I demonstrated how MIES can be used to calculate the budget constraint for each insured in the marketplace. This answered the question – how much insurance can each person afford during each underwriting period?
Although we now have the set of all possible consumption bundles that each person can afford, we still have no method for determining what bundle they will ultimately select – that is, how much insurance will each person actually buy? To answer this question, we turn to the concept of utility. Utility is a measurement of the satisfaction a person receives from a course of action, and we will assume that rational people seek to maximize their utility under scarcity. In this case, the course of action is purchasing insurance, and people seek to maximize their utility subject to the constraint of what they can afford.
Thus, for today’s post I will demonstrate how MIES can assign a utility function to each person in the market and determine each how much insurance each person will purchase.
By introducing utility, I would eventually like to answer certain questions I had about the insurance industry when I thought about building MIES. None of these will be answered today, but this should take us one step closer:
- How much insurance will be purchased in total at market equilibrium?
- Who will go uninsured?
- Should there be a mandatory minimum amount of insurance required by law? If so, should there be a state-run high-risk pool? And if so, how should it be funded?
More detailed treatment of utility can be found in chapters 4 and 5 of Varian.
Utility
To model each person’s preferences for insurance consumption, I’ve decided to use the Cobb-Douglas utility function:
![\[u(x_1, x_2) = x_1^c x_2^d\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-0763177252d9d93761628dd46690e8ad_l3.png "Rendered by QuickLaTeX.com")
Where c and d represent the percentage of income spent on goods 
and 
when 
, and each x represents the quantity of each good. While other utility functions may eventually prove to be more realistic for our simulation, Cobb-Douglas utility functions are a good candidate to start with since they have many convenient features. For example, in order to find the optimal consumption bundle for a person, we need to find the bundle of goods such that the marginal rate of substitution (MRS) equals the slope of the budget constraint, while satisfying the budget constraint itself. For the Cobb-Douglas utility function, Varian provides a derivation for the MRS:
![\[\text{MRS} = -\frac{\partial u(x_1, x_2) / \partial x_1}{\partial u(x_1, x_2) / \partial x_2} \]](https://genedan.com/wp-content/ql-cache/quicklatex.com-93ba278bee63e3fe4c8cc2e29667856a_l3.png "Rendered by QuickLaTeX.com")
This can then be used with the budget constraint, 
, to solve for the quantities of and given the income and price of each good:
![\[x_1 = \frac{c}{c + d}\frac{m}{p_1}\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-4e7c26475288b93f38e711ba6d172711_l3.png "Rendered by QuickLaTeX.com")
![\[x_2 = \frac{d}{c + d} \frac{m}{p_2}\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-5181aa65fa32205703b8f7d0516ce4ca_l3.png "Rendered by QuickLaTeX.com")
and, when , 
and 
. This means that using this result, we can find the optimal consumption bundle algebraically. This is very useful since 1) I have simply forgotten a lot of calculus since leaving school and 2) I won’t have to program calculus into MIES for the time being.
The convexity of the Cobb-Douglas utility function also satisfies certain assumptions underlying consumer behavior. Chapter 3 of Varian provides an in-depth explanation of these assumptions.
Utility Module
I hinted last week that I thought it might be a good idea to break up the econtools.py module into more specific modules. I’ve decided to do this to improve readability and to keep things organized. I’ve created a new folder called econtools to house these modules. The Budget class is now in the budget.py module and the utility function classes are now in a file called utility.py.
The utility.py module contains a single class, called CobbDouglas:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
import plotly.graph_objects as go import numpy as np from plotly.offline import plot class CobbDouglas: def __init__(self, c, d): self.c = c self.d = d def optimal_bundle(self, p1, p2, m): x1_quantity = (self.c / (self.c + self.d)) * (m / p1) x2_quantity = (self.d / (self.c + self.d)) * (m / p2) optimal_utility = (x1_quantity ** self.c) * (x2_quantity ** self.d) return x1_quantity, x2_quantity, optimal_utility def trace(self, k, m): x_values = np.arange(.01, m * 1.5,.01) y_values = (k/(x_values ** self.c)) ** (1/self.d) return {'x': x_values, 'y': y_values, 'mode': 'lines', 'name': 'Utility: ' + str(int(round(k)))} def show_plot(self, k=5, m=10): fig = go.Figure(data=self.trace(k, m)) fig.add_trace(self.trace(k * 1.5, m)) fig.add_trace(self.trace(k * .5, m)) fig['layout'].update({ 'title': 'Cobb Douglas Utility', 'title_x': 0.5, 'xaxis': { 'range': [0, m * 1.5], 'title': 'Amount of Good X' }, 'yaxis': { 'range': [0, m * 1.5], 'title': 'Amount of Good Y' }, 'showlegend': True }) plot(fig) |
The CobbDouglas class takes two arguments, c and d, which correspond to the 
and 
parameters in the function definition. The class provides three methods: optimal_bundle() calculates the optimal consumption bundle using the results derived by Varian, trace() defines the curve as it will appear when plotted, and show_plot() plots the utility function.
Here’s an example on how to use the class to plot the function:
|
1 2 3 4 |
from econtools import CobbDouglas corn_on_the_cobb = CobbDouglas(.5, .5) corn_on_the_cobb.show_plot() |
Here, we’ve provided a simple example where c = d = .5, which means that the consumer will allocate 50% of their income to each good. If the price of each good is the same, the line connecting all optimal consumption bundles will go through the origin (more on that for a later post).
MIES Integration
The Person Class
Now that we’ve got a class defined for our Cobb Douglas function, we now need to find a way to get it working with MIES. I’d like to be able to access the utility function for each consumer in the simulation. Since I’ve started to examine more person-specific characteristics, I’ve created a new class in the entities.py module, Person:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
class Person: def __init__( self, session, engine, person, person_id ): self.session = session self.connection = engine.connect() self.engine = engine self.id = person_id query = self.session.query(person).filter( person.person_id == int(self.id) ).statement self.data = pd.read_sql( query, self.connection ) self.income = self.data['income'].loc[0] self.utility = CobbDouglas( c=self.data['cobb_c'].loc[0], d=self.data['cobb_d'].loc[0] ) self.policy = None self.budget = None self.premium = None self.optimal_bundle = None self.consumption_figure = None def get_policy( self, policy, policy_id ): query = self.session.query(policy).filter( policy.policy_id == int(policy_id) ).statement self.policy = pd.read_sql( query, self.connection ) self.premium = self.policy['premium'].loc[0] def get_budget(self): all_other = Good(1, name='All Other Goods') if self.policy is None: insurance = Good(4000, name='Insurance') else: insurance = Good(self.premium, name='Insurance') self.budget = Budget(insurance, all_other, income=self.income, name='Budget') def get_consumption(self): self.optimal_bundle = self.utility.optimal_bundle( p1=self.premium, p2=1, m=self.income ) def get_consumption_figure(self): fig = go.Figure() fig.add_trace(self.budget.get_line()) fig.add_trace(self.utility.trace(k=self.optimal_bundle[2], m=self.income / self.premium * 1.5)) fig.add_trace(self.utility.trace(k=self.optimal_bundle[2] * 1.5, m=self.income / self.premium * 1.5)) fig.add_trace(self.utility.trace(k=self.optimal_bundle[2] * .5, m=self.income / self.premium * 1.5)) fig['layout'].update({ 'title': 'Consumption for Person ' + str(self.id), 'title_x': 0.5, 'xaxis': { 'title': 'Amount of Insurance', 'range': [0, self.income / self.premium * 1.5] }, 'yaxis': { 'title': 'Amount of All Other Goods', 'range': [0, self.income * 1.5] } }) self.consumption_figure = fig return fig def show_consumption(self): plot(self.consumption_figure) |
Since there is already a Person class in the schema.py module referencing a SQLite table, I’ve renamed that class to PersonTable. The Person class takes a database connection, along with the person table in the database, queries the details of a person, and generates a utility function for that person. The Person class provides additional methods for attaching policy information, calculating that person’s budget, and determining how much insurance they will buy.
To keep things simple, I’ve assumed that each person’s parameter equals, .1, which means that the population has homogeneous preferences for insurance, and will spend 10% of their income on it. The parameters.py module and environment class have been updated accordingly to reflect this. We can loosen these assumptions later on.
Optimal Consumption
Let’s find one person’s optimal bundle for purchasing insurance. To do this, we run two iterations of the simulation and examine the results for person_id = 1, like we did last week:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import pandas as pd import datetime as dt import sqlalchemy as sa import econtools as ec from SQLite.schema import PersonTable, Policy, Base, Company, Event from sqlalchemy.orm import sessionmaker from entities import God, Broker, Insurer, Person import numpy as np import plotly.graph_objects as go from plotly.offline import plot pd.set_option('display.max_columns', None) engine = sa.create_engine('sqlite:///MIES_Lite.db', echo=True) Session = sessionmaker(bind=engine) Base.metadata.create_all(engine) gsession = Session() ahura = God(gsession, engine) ahura.make_population(1000) pricing_date = dt.date(1, 12, 31) rayon = Broker(gsession, engine) company_1 = Insurer(gsession, engine, 4000000, Company, 'company_1') company_1_formula = 'severity ~ age_class + profession + health_status + education_level' pricing_status = 'initial_pricing' free_business = rayon.identify_free_business(PersonTable, Policy, pricing_date) companies = pd.read_sql(gsession.query(Company).statement, engine.connect()) rayon.place_business(free_business, companies, pricing_status, pricing_date, company_1) ahura.smite(PersonTable, Policy, pricing_date + dt.timedelta(days=1)) company_1.price_book(PersonTable, Policy, Event, company_1_formula) pricing_status = 'renewal_pricing' rayon.place_business(free_business, companies, pricing_status, pricing_date, company_1) |
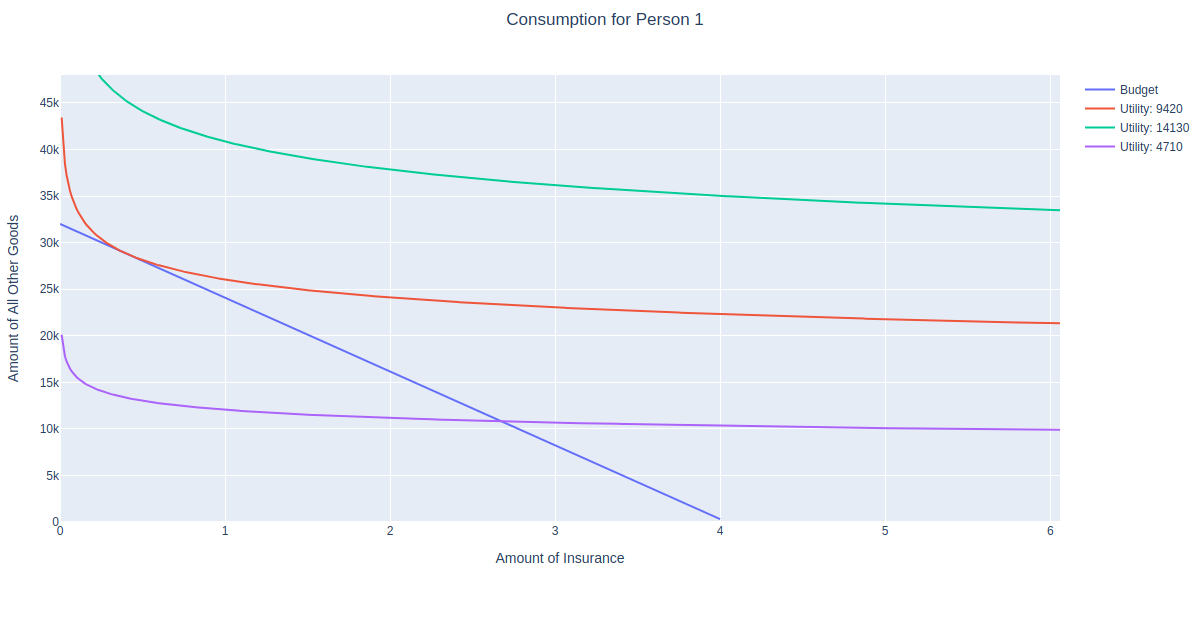
This person has an income of about 32k. You can also see additional columns for their Cobb Douglas parameters. If all goes well, we would expect them to want to spend about 3200 on insurance. Let’s query their renewal quote to see how much premium they need to pay:
|
1 2 |
my_person = Person(session=gsession, engine=engine, person=PersonTable, person_id=1) my_person.get_policy(Policy, 1001) |
Since their premium is about 8k, we’d expect them to consume roughly 3.2/8 = .4 units of insurance upon renewal. Let’s solve for their optimal bundle to confirm:
|
1 2 3 |
my_person.get_budget() my_person.get_consumption() my_person.get_consumption_figure() |
Indeed, the point of tangency between the budget constraint and red utility curve is around .4 (ish) units of insurance. Interestingly, since the insured will only purchase .4 units of insurance upon renewal, they are no longer fully insured. From an actuarial standpoint, it is desirable for customers to fully insure things like homes, and a penalty is typically built into the premium if a customer decides not to do so. More on that topic (much) later.
Further Improvements
I’ve introduced quite a few concepts into the consumption aspect of MIES, and have yet to rerun the simulation for more than two iterations. Before I can do this, I’ll need to revise certain aspects of the insureds, such as personal wealth, and partial insurance. I have not even incorporated wealth for each person, so the idea of having only part of it covered under the case of partial insurance currently has no meaning.
Appendix: SymPy
Since the optimization problem discussed here involves calculus, I thought maybe I should eventually have some calculus programmed in MIES. There’s a library called SymPy that facilitates symbolic computation in Python. Let’s try it out by computing the partial derivatives of the Cobb-Douglas utility function, required to solve for the MRS:
|
1 2 3 4 5 6 7 |
from sympy import symbols, diff c, d, x1, x2 = symbols('c d x1 x2') u = (x1 ** c) * (x2 ** d) mrs = -diff(u, x1) / diff(u, x2) print(mrs) |
The console prints -c*x2/(d*x1), which is MRS = 
, the same as that derived in Varian. That looks pretty useful. However, Sympy’s documentation is massive, at over 2000 pages. It might take some time to learn it, even if it just involves me grabbing what I need. Since I can make do without calculus for the time being, I’ll save this for another day.