This entry is part of a series dedicated to MIES – a miniature insurance economic simulator. The source code for the project is available on GitHub.
Current Status
Last week, I revisited the MIES backend to split what was a single database into multiple databases – one per entity in the simulation. This enhances the level of realism and should make it easier to program transactions between the entities. This week, I’ll revisit consumer behavior by implementing the Slutsky and Hicks decomposition methods for analyzing price changes.
In the context of insurance, consumers frequently experience changes in price, typically during renewals when insurers apply updated rating algorithms against new information known about the insureds. For example, If you’ve made a claim or two during your policy period, and miss a rent payment, causing your credit score to go down, your premium is likely to increase upon renewal. This is because past claims and credit are frequently used as the underlying variables in a rating algorithm.
What happens when consumers face an increase in rates? Oftentimes, they reduce coverage, may try to shop around, or may do nothing at all and simply pay the new price. Today’s post discusses the first phenomenon, whereby an increase in rates causes a reduction in the amount of insurance that a consumer purchases. We can use the Slutsky and Hicks decomposition methods to break down this behavior into two components:
- The substitution effect
- The income effect
The substitution effect concerns the change in relative prices between two goods. Here, when a consumer faces a premium increase, the price of insurance increases relative to the price of all other goods, altering the rate at which the consumer would be willing to exchange a unit of insurance for a unit of all other goods.
The income effect concerns the change in the price of a good relative to consumer income. When a consumer faces a premium increase without a corresponding increase in income, their income affords them fewer units of insurance.
The content of this post roughly follows the content of chapter 8 in Varian. As usual, I focus on how this applies to my own project and will skip over much of the theoretical derivations that can be found in the text.
Slutsky Identity
The Slutsky identity has the following form:
![\[\frac{\Delta x_1}{\Delta p_1} = \frac{\Delta x_1^s}{\Delta p_1} - \frac{\Delta x_1^m}{\Delta m}x_1\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-267df81a1e9f4fd29a64d1fdaf119964_l3.png "Rendered by QuickLaTeX.com")
Where the 
represents the quantity of good 1 (in this case insurance), 
represents the price of insurance (that is, the premium) and 
represents the consumer’s income. The deltas are used to describe how the quantity of insurance purchased changes with premium, expressed on the left side of the identity. The first term after the equals sign represents the substitution effect, and the second term after the equals sign represents the income effect.
The Slutsky identity can also be expressed in terms of units instead of rates of change (
):
![\[\Delta x_1 = \Delta x_1^s + \Delta x_1^n\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-7b29a37678e0e5699894f293d45692e6_l3.png "Rendered by QuickLaTeX.com")
While MIES can handle both forms, we’ll focus on the first form for the rest of the chapter.
Substitution Effect
Let’s examine the substitution effect. First, we’ll conduct all the steps manually, and then I’ll show how they are integrated into MIES. If we have some data already stored in a past simulation, we can extract a person from it:
|
1 2 |
my_person = Person(1) my_person.data |
|
1 2 3 4 5 |
Out[12]: person_id age_class profession health_status education_level income \ 0 1 E B F U 89023.365436 wealth cobb_c cobb_d 0 225300.272033 0.1 0.9 |
Here, we have a person who makes 89k per year, with Cobb Douglas parameters c = 0.1 and d = 0.9. This means this person will spend 10% of their income on premium. For the sake of making the graphs in this post less cluttered and easier to read, let’s change c = d = .5 so the person spends 50% of their income on insurance:
|
1 2 3 4 5 6 |
my_person.utility.c = .5 my_person.utility.d = .5 my_person.get_budget() my_person.get_consumption() my_person.get_consumption_figure() my_person.show_consumption() |
From the above figure, we can see that the person consumes about 45k worth of insurance. That’s about 11 units of exposure at a 4k premium per exposure, which is unrealistic in real life, but makes life easy for me because I haven’t bothered to update the margins of my website to accommodate wider figures. We’ll denote this bundle as ‘Old Bundle’ because we’ll compare it to the new consumption bundle after a rate change (note – if you are trying to replicate this in MIES, your figures may look a bit different, in reality I manually adjust the style of the plots so they can fit on my blog).
Now, let’s suppose the person faces a 100% increase in their rate so that their premium is 8k per unit of exposure, and construct a budget to reflect this:
|
1 2 3 |
insurance = Good(8000, name='insurance') all_other = Good(1, name='all other goods') new_budget = Budget(insurance, all_other, income=my_person.income, name='new_budget') |
Plotting this new budget, we see that the line tilts inward, since the person can only afford half as much insurance as before:
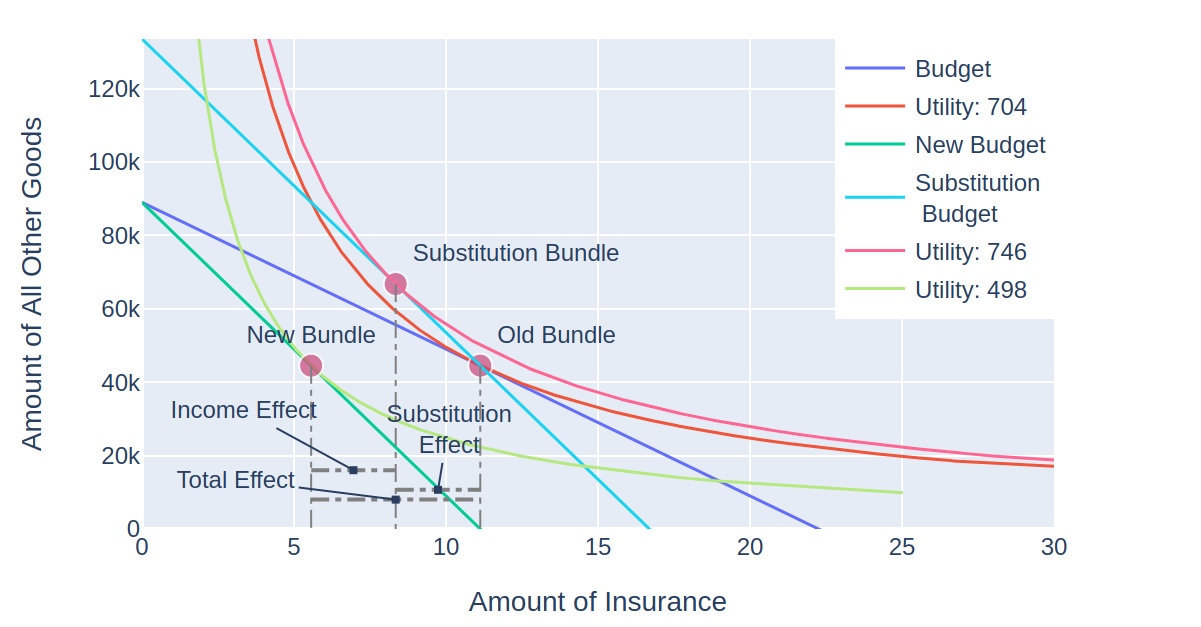
The first stage in Slutsky decomposition involves calculating the substitution effect. This is done by tilting the budget line to the slope of the new prices, but with income adjusted so that the person can still afford their old bundle. We then determine the new optimal bundle at this budget (denoted ‘substitution budget’) and call it the substitution bundle:
![\[\Delta m = x_1 \Delta p_1\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-31da15f60d083e8875f089826d8cb193_l3.png "Rendered by QuickLaTeX.com")
|
1 2 3 |
sub_income = my_person.income + my_person.optimal_bundle[0] * 4000 substitution_budget = Budget(insurance, all_other, income=sub_income, name='Substitution<br /> Budget') ...more plotting code... |
You can see that if the person were given enough money to purchase the same amount of insurance even after the rate increase, they would still reduce their consumption from 11.1 to 8.3 units of insurance. 8.3 – 11.1 = -2.8 is the substitution effect.
Income Effect
Now, to calculate the income effect, we then shift the substitution budget to the position of the new budget:
The person purchases 5.5 units of insurance at the new budget, so the income effect is 5.5 – 8.3 = -2.8 for the substitution effect. The total effect is -2.8 -2.8 = -5.6 units of insurance, the sum of the substitution and income effect. This is the same as the new consumption minus the old consumption 5.5 – 11.1 = -5.6
MIES Integration
The Slutsky decomposition process has been integrated into MIES as a class in econtools/slutsky.py:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 |
import plotly.graph_objects as go from plotly.offline import plot from econtools.budget import Budget from econtools.utility import CobbDouglas class Slutsky: """ Implementation of the Slutsky equation, accepts two budgets, a utility function, and calculates the income and substitution effects """ def __init__( self, old_budget: Budget, new_budget: Budget, utility_function: CobbDouglas # need to replace with utility superclass ): self.old_budget = old_budget self.old_budget.name = 'Old Budget' self.new_budget = new_budget self.new_budget.name = 'New Budget' self.utility = utility_function self.old_bundle = self.utility.optimal_bundle( self.old_budget.good_x.price, self.old_budget.good_y.price, self.old_budget.income ) self.delta_p = self.new_budget.good_x.price - self.old_budget.good_x.price self.pivoted_budget = self.calculate_pivoted_budget() self.substitution_bundle = self.calculate_substitution_bundle() self.substitution_effect = self.calculate_substitution_effect() self.new_bundle = self.calculate_new_bundle() self.income_effect = self.calculate_income_effect() self.total_effect = self.substitution_effect + self.income_effect self.substitution_rate = self.calculate_substitution_rate() self.income_rate = self.calculate_income_rate() self.slutsky_rate = self.substitution_rate - self.income_rate self.plot = self.get_slutsky_plot() def calculate_pivoted_budget(self): """ Pivot the budget line at the new price so the consumer can still afford their old bundle """ delta_m = self.old_bundle[0] * self.delta_p pivoted_income = self.old_budget.income + delta_m pivoted_budget = Budget( self.new_budget.good_x, self.old_budget.good_y, pivoted_income, 'Pivoted Budget' ) return pivoted_budget def calculate_substitution_bundle(self): """ Return the bundle consumed after pivoting the budget line """ substitution_bundle = self.utility.optimal_bundle( self.pivoted_budget.good_x.price, self.pivoted_budget.good_y.price, self.pivoted_budget.income ) return substitution_bundle def calculate_substitution_effect(self): substitution_effect = self.substitution_bundle[0] - self.old_bundle[0] return substitution_effect def calculate_new_bundle(self): """ Shift the budget line outward """ new_bundle = self.utility.optimal_bundle( self.new_budget.good_x.price, self.new_budget.good_y.price, self.new_budget.income ) return new_bundle def calculate_income_effect(self): income_effect = self.new_bundle[0] - self.substitution_bundle[0] return income_effect def calculate_substitution_rate(self): delta_s = self.calculate_substitution_effect() delta_p = self.new_budget.good_x.price - self.old_budget.good_x.price substitution_rate = delta_s / delta_p return substitution_rate def calculate_income_rate(self): delta_p = self.new_budget.good_x.price - self.old_budget.good_x.price delta_m = self.old_bundle[0] * delta_p delta_x1m = -self.calculate_income_effect() income_rate = delta_x1m / delta_m * self.old_bundle[0] return income_rate def get_slutsky_plot(self): max_x_int = max( self.old_budget.income / self.old_budget.good_x.price, self.pivoted_budget.income / self.pivoted_budget.good_x.price, self.new_budget.income / self.new_budget.good_x.price ) * 1.2 max_y_int = max( self.old_budget.income, self.pivoted_budget.income, self.new_budget.income, ) * 1.2 # interval boundaries effect_boundaries = [ self.new_bundle[0], self.substitution_bundle[0], self.old_bundle[0] ] effect_boundaries.sort() fig = go.Figure() # budget lines fig.add_trace(self.old_budget.get_line()) fig.add_trace(self.pivoted_budget.get_line()) fig.add_trace(self.new_budget.get_line()) # utility curves fig.add_trace( self.utility.trace( k=self.old_bundle[2], m=max_x_int, name='Old Utility' ) ) fig.add_trace( self.utility.trace( k=self.substitution_bundle[2], m=max_x_int, name='Pivoted Utility' ) ) fig.add_trace( self.utility.trace( k=self.new_bundle[2], m=max_x_int, name='New Utility' ) ) # consumption bundles fig.add_trace( go.Scatter( x=[self.old_bundle[0]], y=[self.old_bundle[1]], mode='markers+text', text=['Old Bundle'], textposition='top center', marker=dict( size=[15], color=[1] ), showlegend=False ) ) fig.add_trace( go.Scatter( x=[self.substitution_bundle[0]], y=[self.substitution_bundle[1]], mode='markers+text', text=['Pivoted Bundle'], textposition='top center', marker=dict( size=[15], color=[2] ), showlegend=False ) ) fig.add_trace( go.Scatter( x=[self.new_bundle[0]], y=[self.new_bundle[1]], mode='markers+text', text=['New Bundle'], textposition='top center', marker=dict( size=[15], color=[3] ), showlegend=False ) ) # Substitution and income effect interval lines fig.add_shape( type='line', x0=self.substitution_bundle[0], y0=self.substitution_bundle[1], x1=self.substitution_bundle[0], y1=0, line=dict( color="grey", dash="dashdot", width=1 ) ) fig.add_shape( type='line', x0=self.new_bundle[0], y0=self.new_bundle[1], x1=self.new_bundle[0], y1=0, line=dict( color="grey", dash="dashdot", width=1 ) ) fig.add_shape( type='line', x0=self.old_bundle[0], y0=self.old_bundle[1], x1=self.old_bundle[0], y1=0, line=dict( color="grey", dash="dashdot", width=1 ) ) fig.add_shape( type='line', xref='x', yref='y', x0=effect_boundaries[0], y0=max_y_int / 10, x1=effect_boundaries[1], y1=max_y_int / 10, line=dict( color='grey', dash='dashdot' ) ) fig.add_shape( type='line', xref='x', yref='y', x0=effect_boundaries[1], y0=max_y_int / 15, x1=effect_boundaries[2], y1=max_y_int / 15, line=dict( color='grey', dash='dashdot' ) ) fig.add_shape( type='line', xref='x', yref='y', x0=effect_boundaries[0], y0=max_y_int / 20, x1=effect_boundaries[2], y1=max_y_int / 20, line=dict( color='grey', dash='dashdot' ) ) fig.add_annotation( x=(self.substitution_bundle[0] + self.old_bundle[0]) / 2, y=max_y_int / 10, text='Substitution<br />Effect', xref='x', yref='y', showarrow=True, arrowhead=7, ax=5, ay=-40, ) fig.add_annotation( x=(self.new_bundle[0] + self.substitution_bundle[0]) / 2, y=max_y_int / 15, text='Income Effect', xref='x', yref='y', showarrow=True, arrowhead=7, ax=50, ay=-20 ) fig.add_annotation( x=(effect_boundaries[2] + effect_boundaries[0]) / 2, y=max_y_int / 20, text='Total Effect', xref='x', yref='y', showarrow=True, arrowhead=7, ax=100, ay=20 ) fig['layout'].update({ 'title': 'Slutsky Decomposition', 'title_x': 0.5, 'xaxis': { 'title': 'Amount of Insurance', 'range': [0, max_x_int] }, 'yaxis': { 'title': 'Amount of All Other Goods', 'range': [0, max_y_int] } }) return fig def show_plot(self): plot(self.plot) |
This has been added to the Person class, so we can use its methods to get the substitution and income effects. This conveniently packages all the manual steps we took above together:
|
1 2 3 |
my_person.calculate_slutsky(new_budget) my_person.slutsky.income_effect my_person.slutsky.substitution_effect |
Which returns -2.8 for each effect, the same as above.
Hicks Decomposition
A similar decomposition method is called Hicks decomposition. Instead of pivoting the budget constraint so that the person can afford the same bundle as before, the budget constraint is shifted so that they have the same utility as before. Using algebra, we can solve this by fixing utility:
![\[m^\prime = \frac{\bar{u}}{\left(\frac{c}{c +d}\frac{1}{p_1^\prime}\right)^c\left(\frac{d}{c+d}\frac{1}{p_2}\right)^d}\]](https://genedan.com/wp-content/ql-cache/quicklatex.com-7b6922ae6c1c86720257822287c6dbc6_l3.png "Rendered by QuickLaTeX.com")
where 
is the adjusted income, and 
is the new premium, and 
is the utility fixed at the original level.
You’ll notice there’s a subtle difference, the new bundle is the same as in the Slutsky case, but the substitution bundle in this case is on the original utility curve. This gives different answers for the substitution and income effects, which are -3.3 and -2.3, which add up to a total effect of -5.6, as before.
The code for the Hicks class is much the same as that for the Slutsky class, so I won’t post most of it here, the relevant change is in calculating the substitution budget:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class Hicks: ... def calculate_pivoted_budget(self): """ Pivot the budget line at the new price so the consumer still as the same utility """ old_utility = self.old_bundle[2] c = self.utility.c d = self.utility.d p1_p = self.new_budget.good_x.price p2 = self.old_budget.good_y.price x1_no_m = (((c / (c + d)) * (1 / p1_p)) ** c) x2_no_m = (((d / (c + d)) * (1 / p2)) ** d) pivoted_income = old_utility / (x1_no_m * x2_no_m) pivoted_budget = Budget( self.new_budget.good_x, self.old_budget.good_y, pivoted_income, 'Pivoted Budget' ) return pivoted_budget ... |
Further Improvements
Since Hicks substitution is mostly similar to Slutsky in terms of code, it makes sense for the Hicks class to inherit from the Slutsky class or for both of them to inherit from a superclass.
I’m currently working on implementing wealth into MIES, since as of today, none of the transactions actually impact wealth.