Today marks an exciting new milestone with the release of FASLR v0.0.2. FASLR (Free Actuarial System for Loss Reserving), is an open-source frontend for loss reserving packages, such as the chainladder package on the Casualty Actuarial Society’s GitHub. As far as I can tell, it’s the first system of its kind – one that will give the actuary full insight into the loss reserving process, from data ingestion to final-sign off, with all the calculations being fully transparent since the source code is freely available.
Last time, I demonstrated that FASLR was able to conduct the most basic loss reserving method, the chain ladder technique. Today I’d like to walk you though some important improvements, the first of which adds new ways to view and arrange triangle data within the program, and the other, which enhances FASLR with diagnostic techniques used to test the assumptions of the chain ladder method.
New features added in v.0.0.2:
- Analysis pane for viewing different cuts of triangle data
- Mack diagnostic tests
- Valuation correlation test across all periods
- Valuation correlation test for individual periods
- Development correlation test
The Analysis Pane
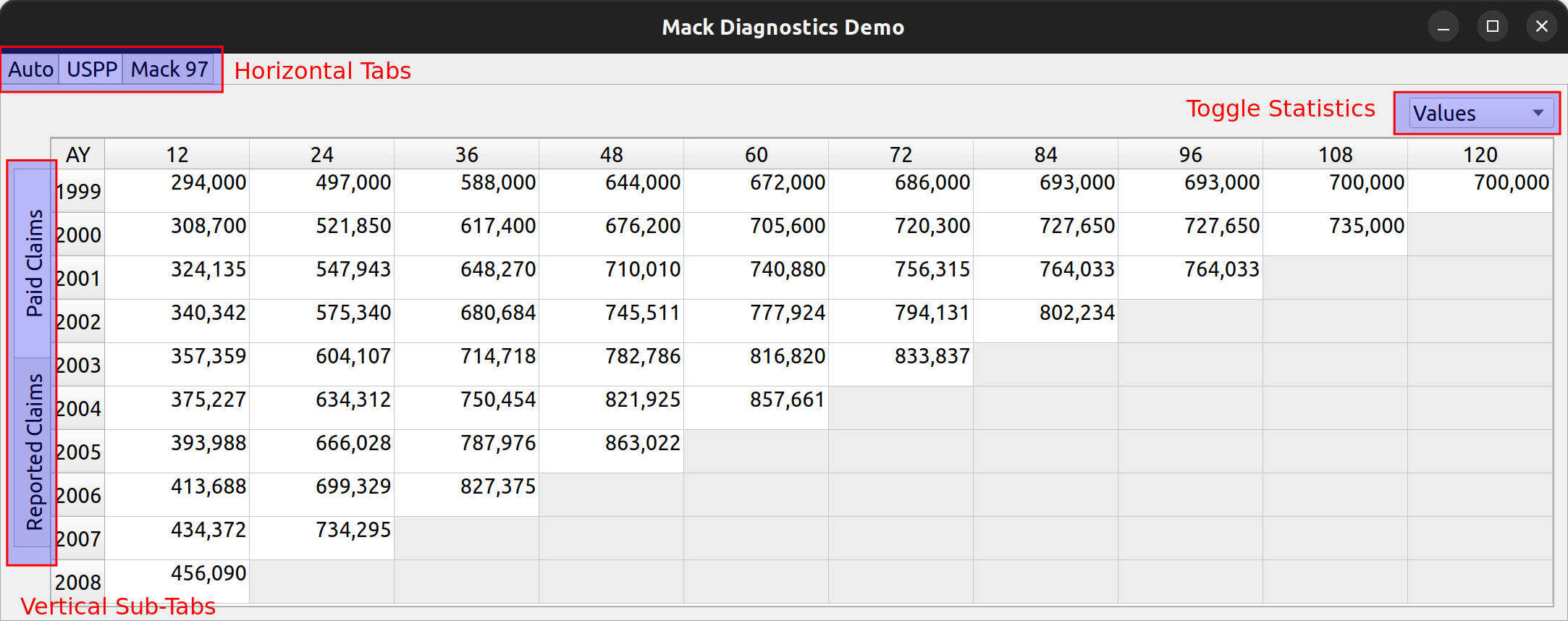
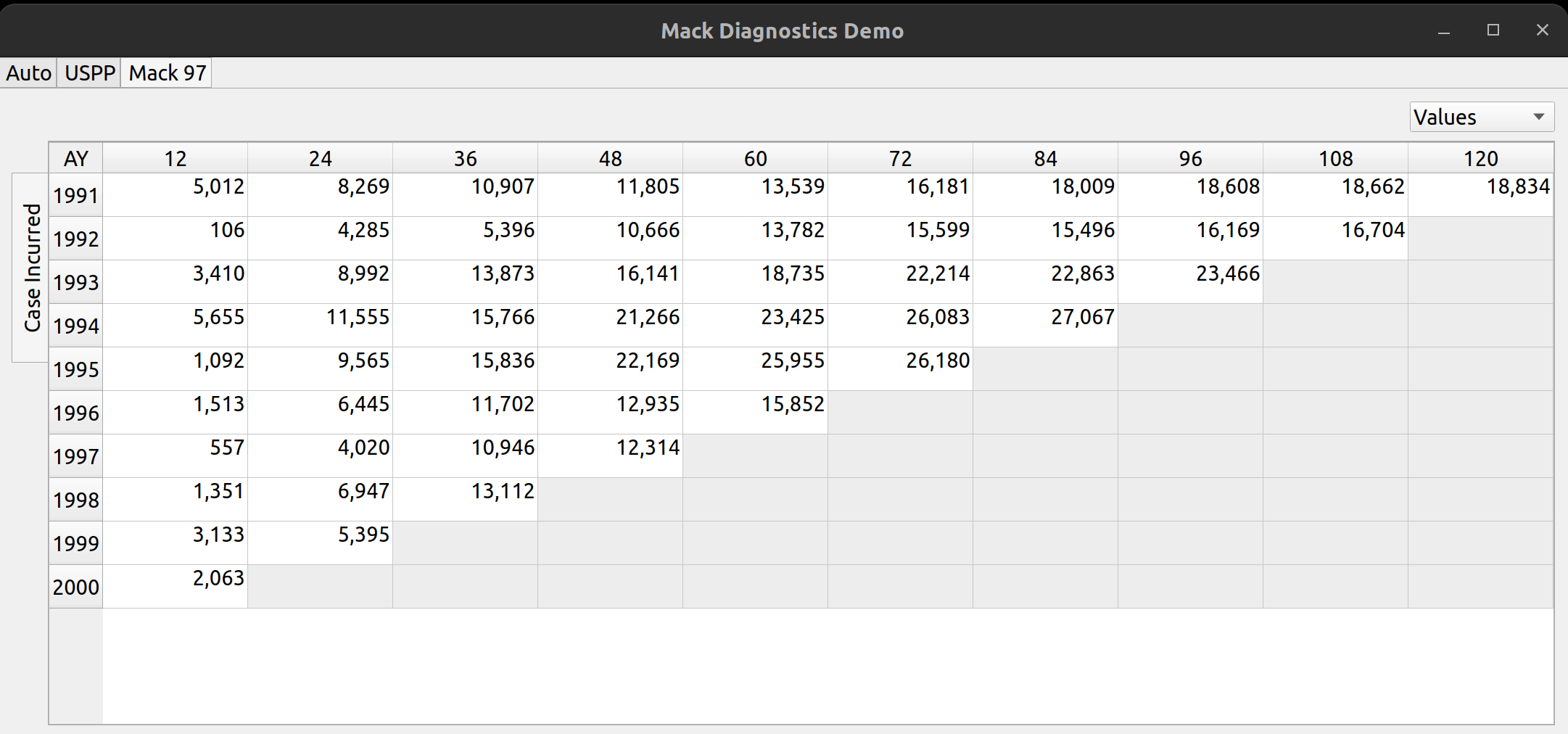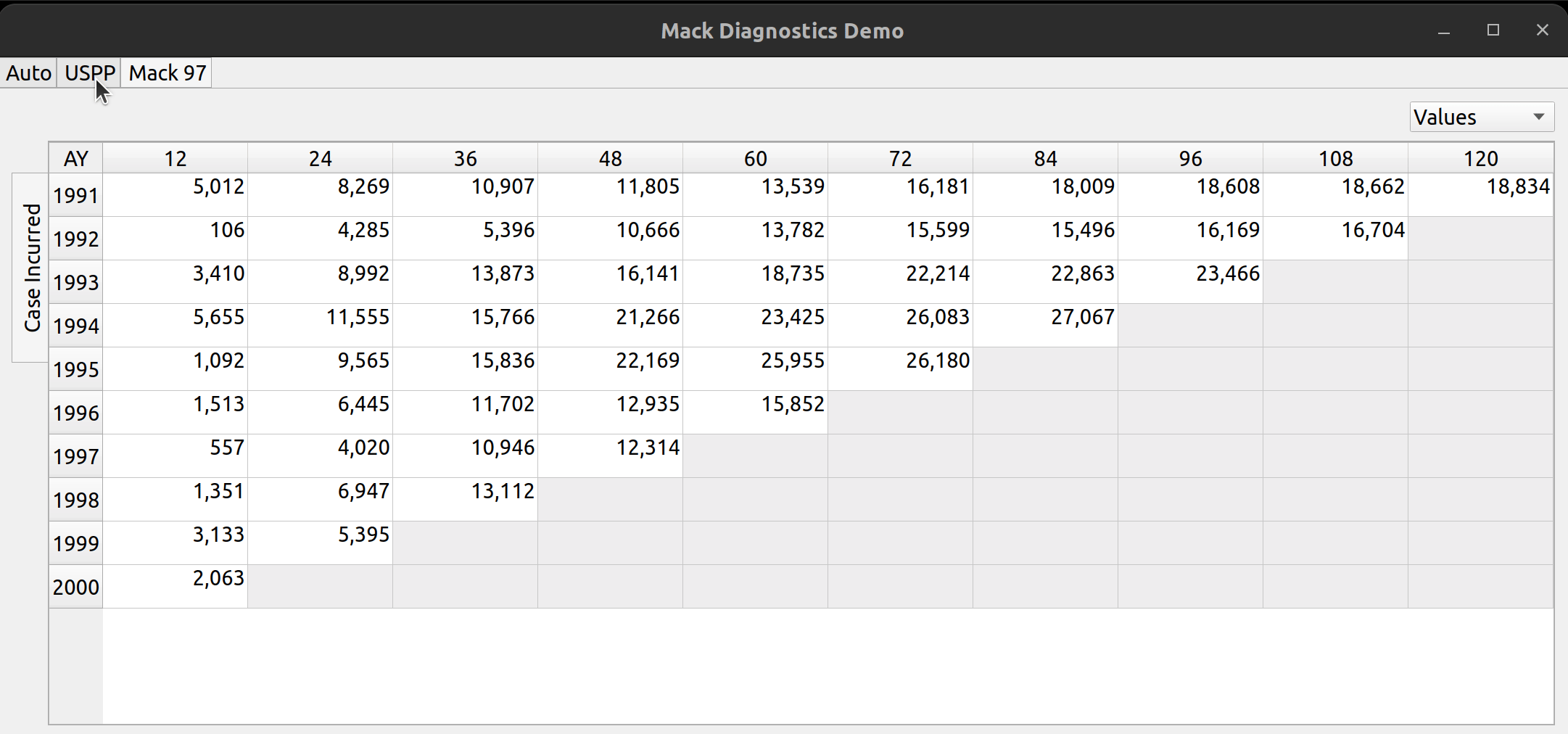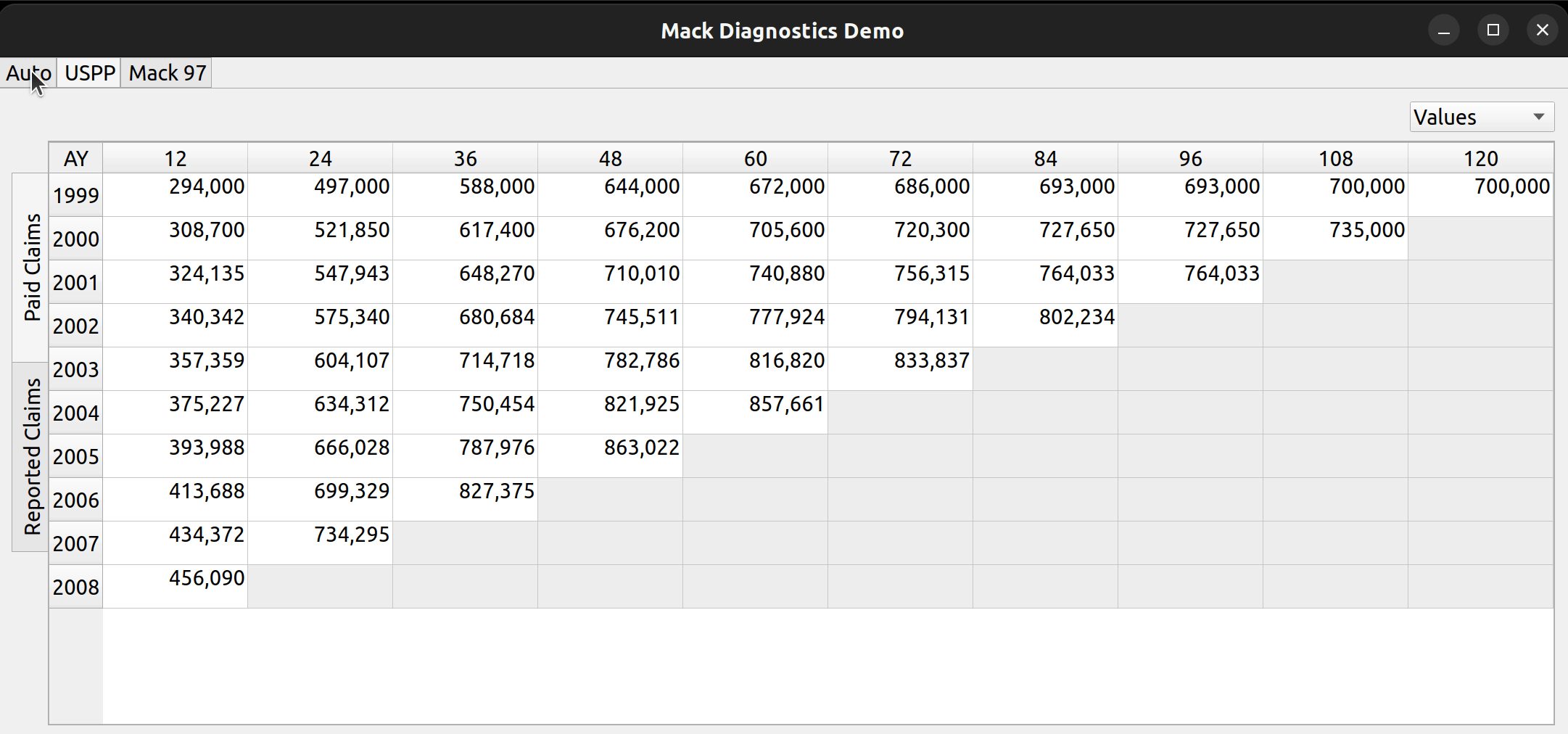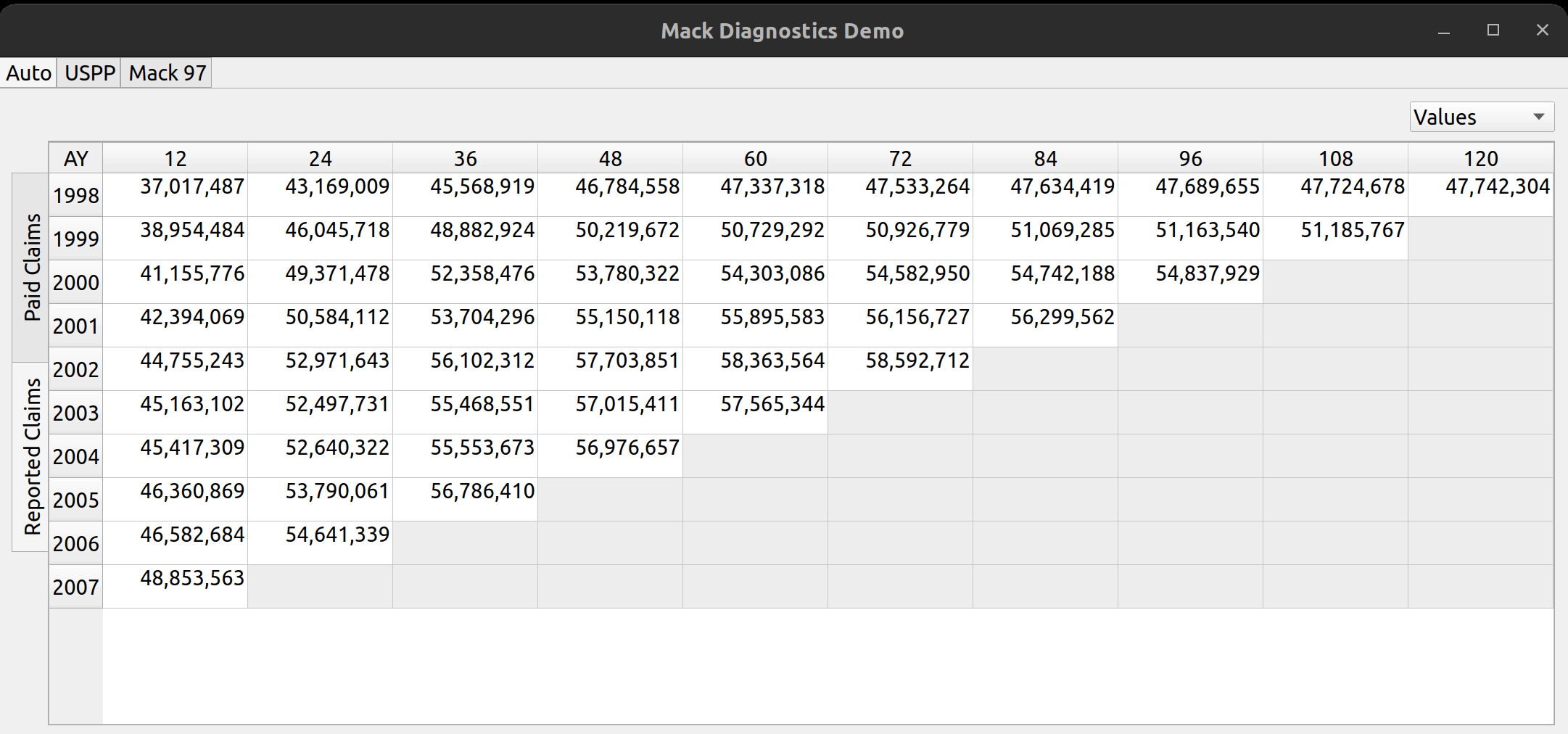
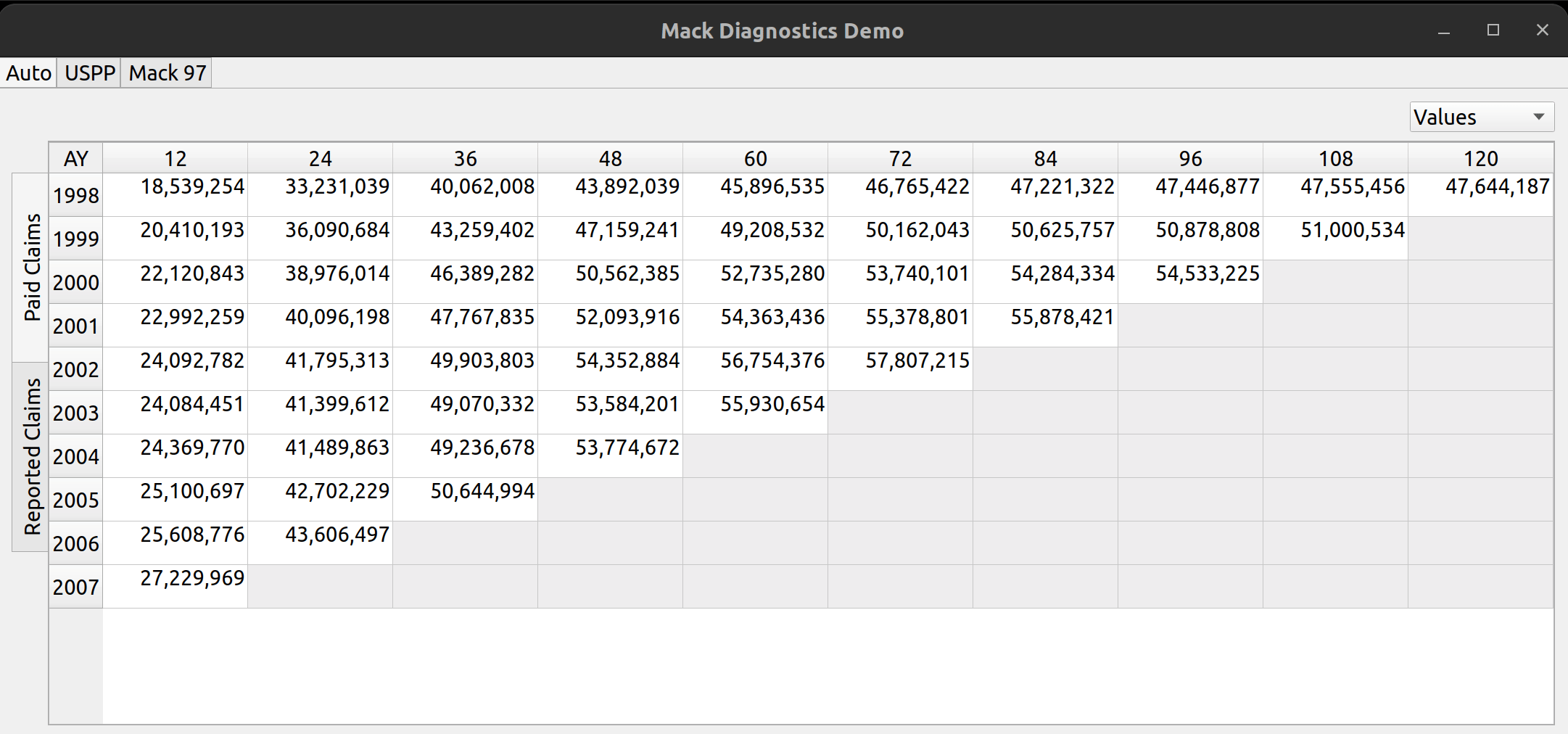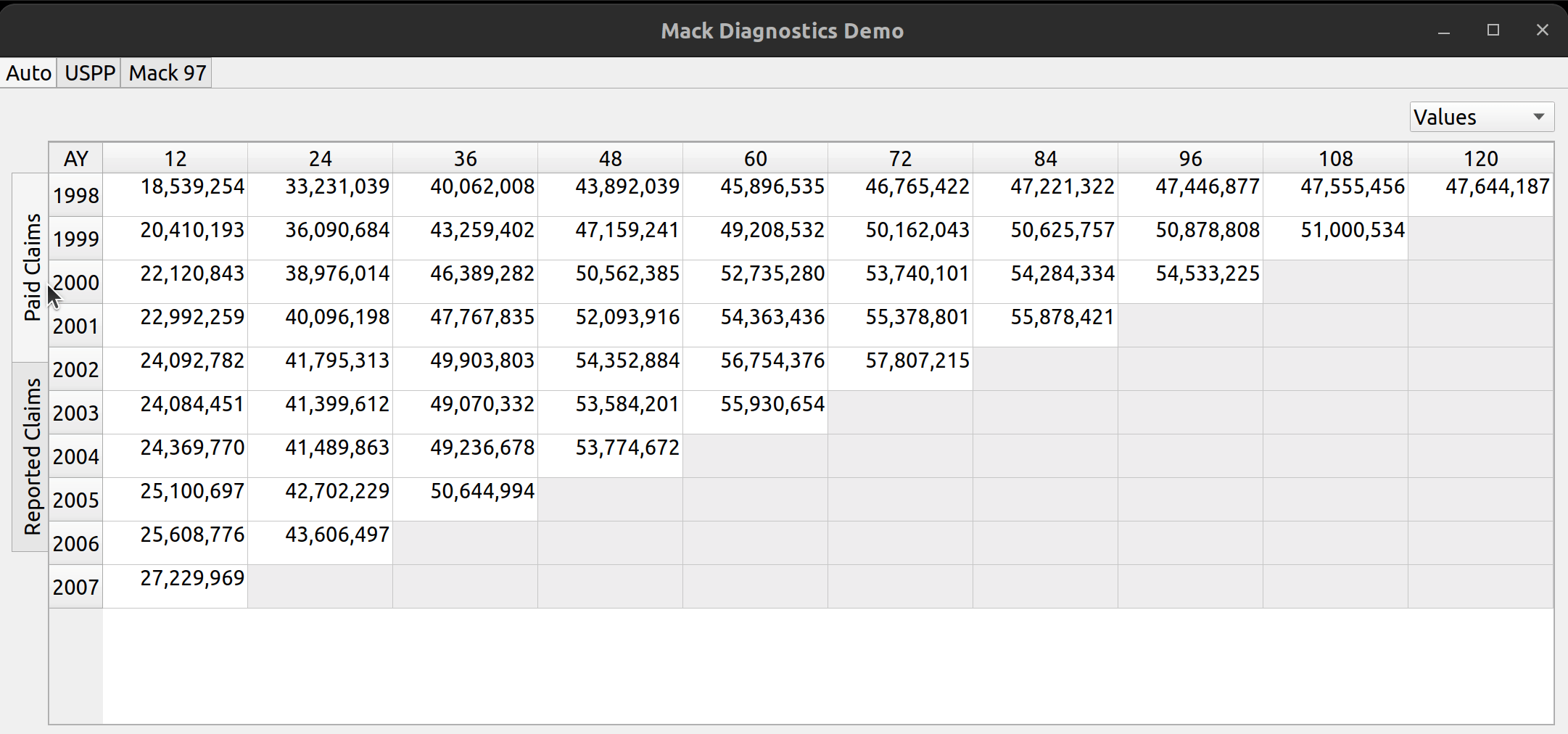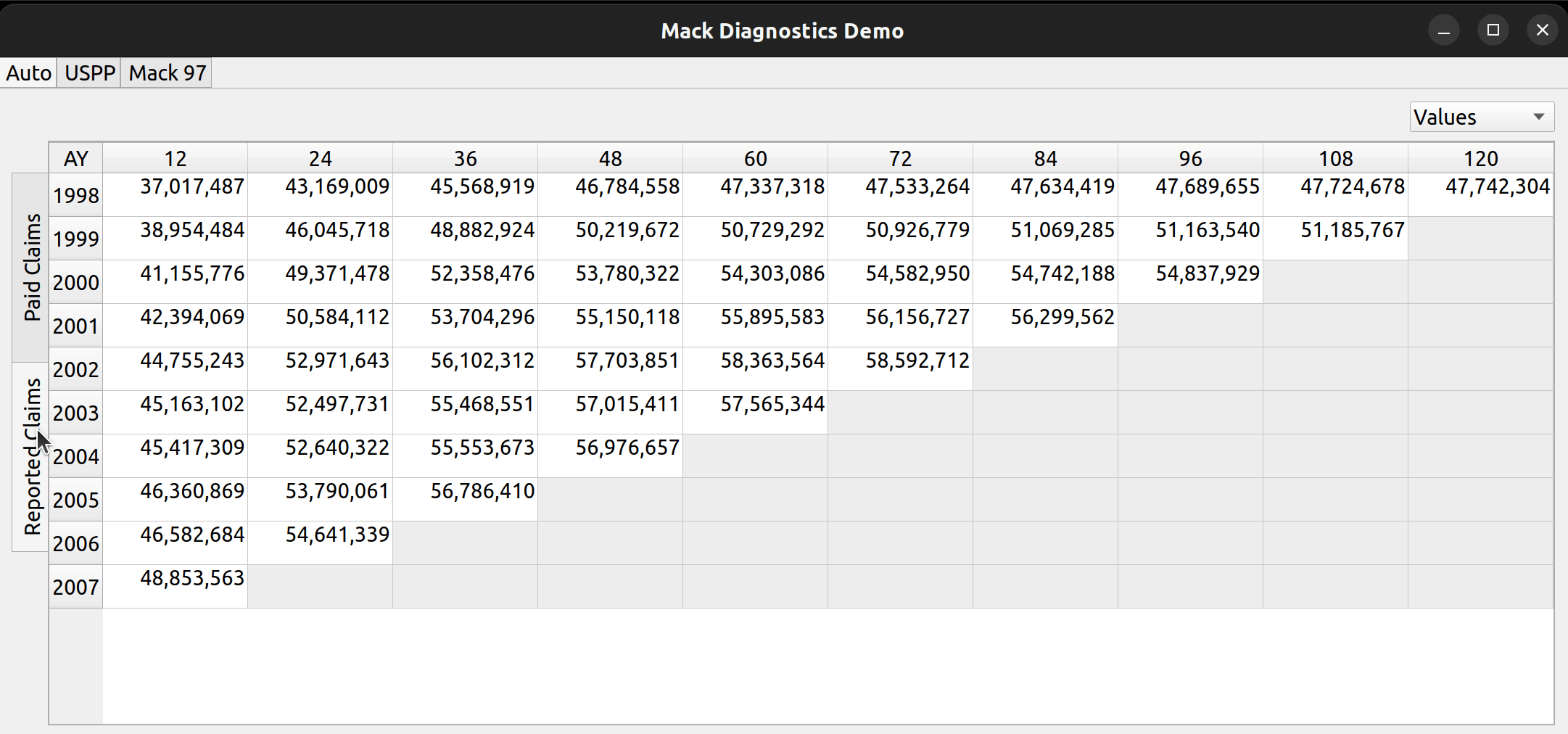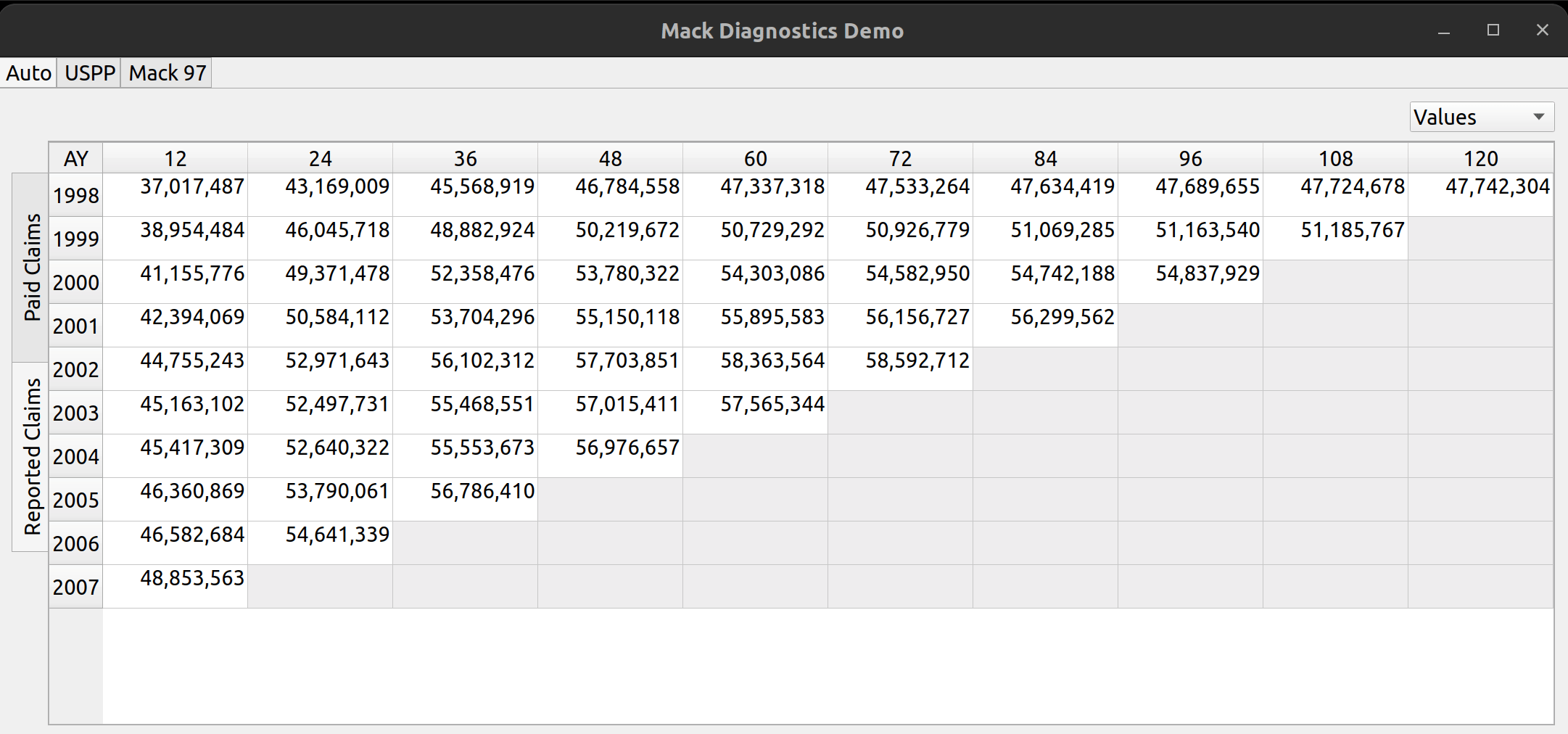
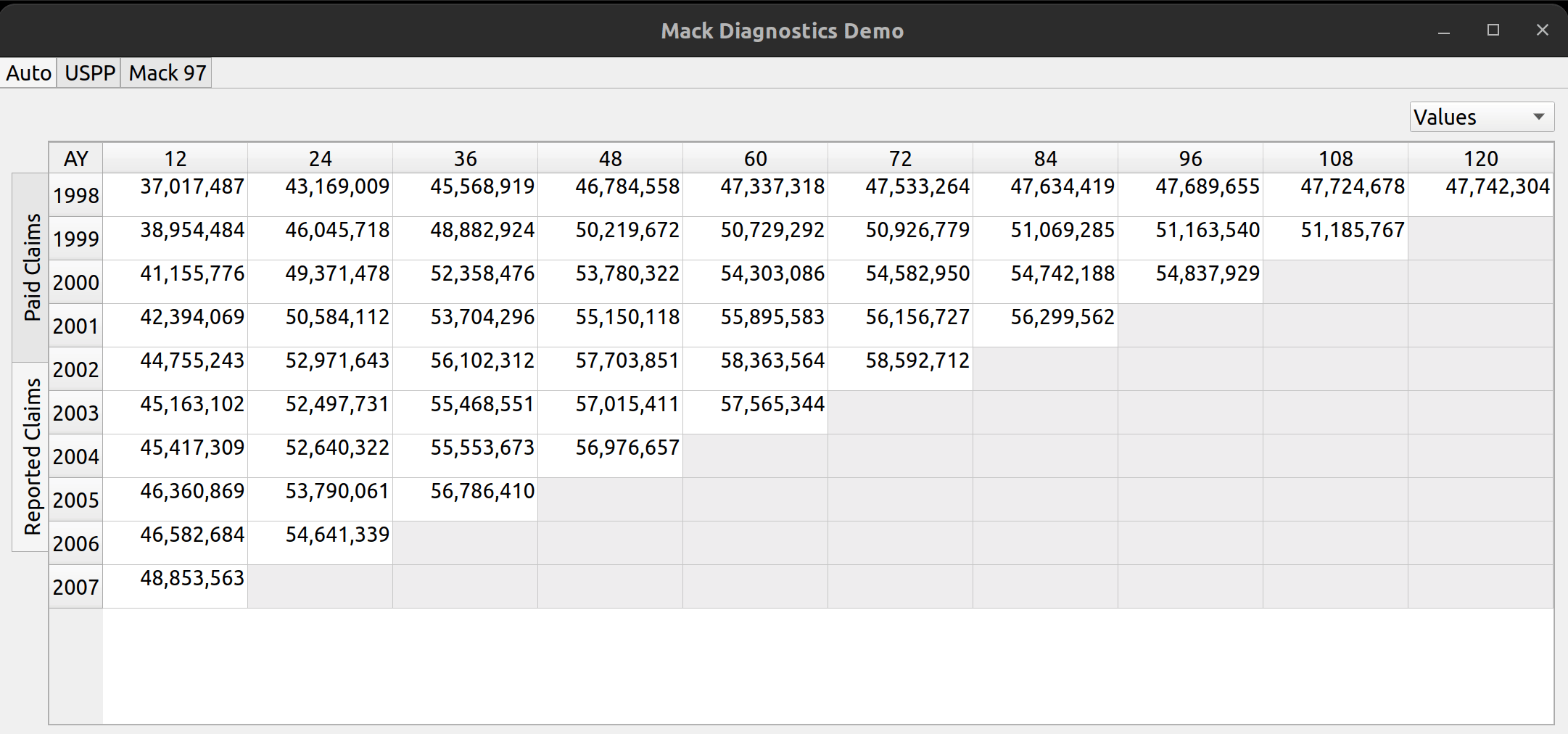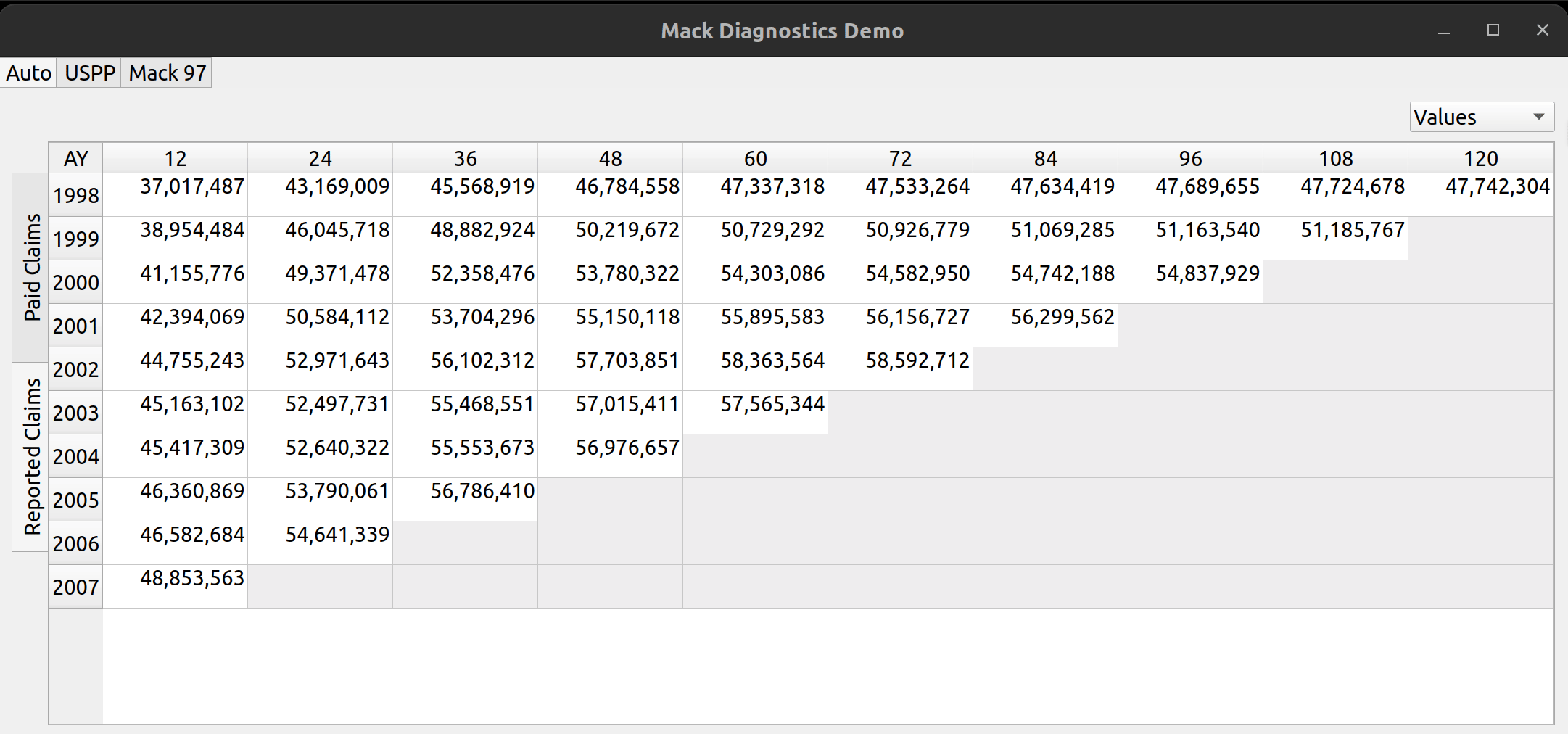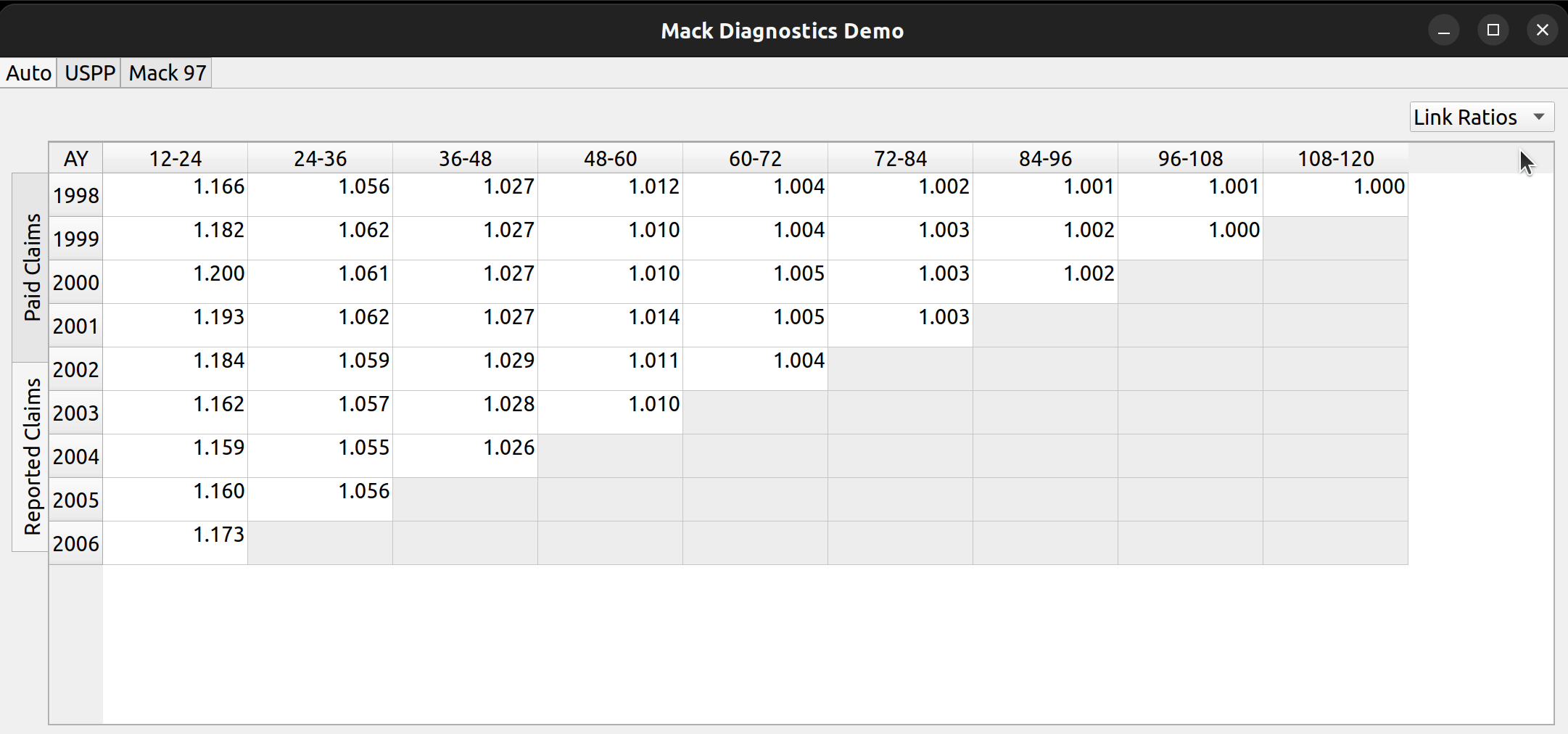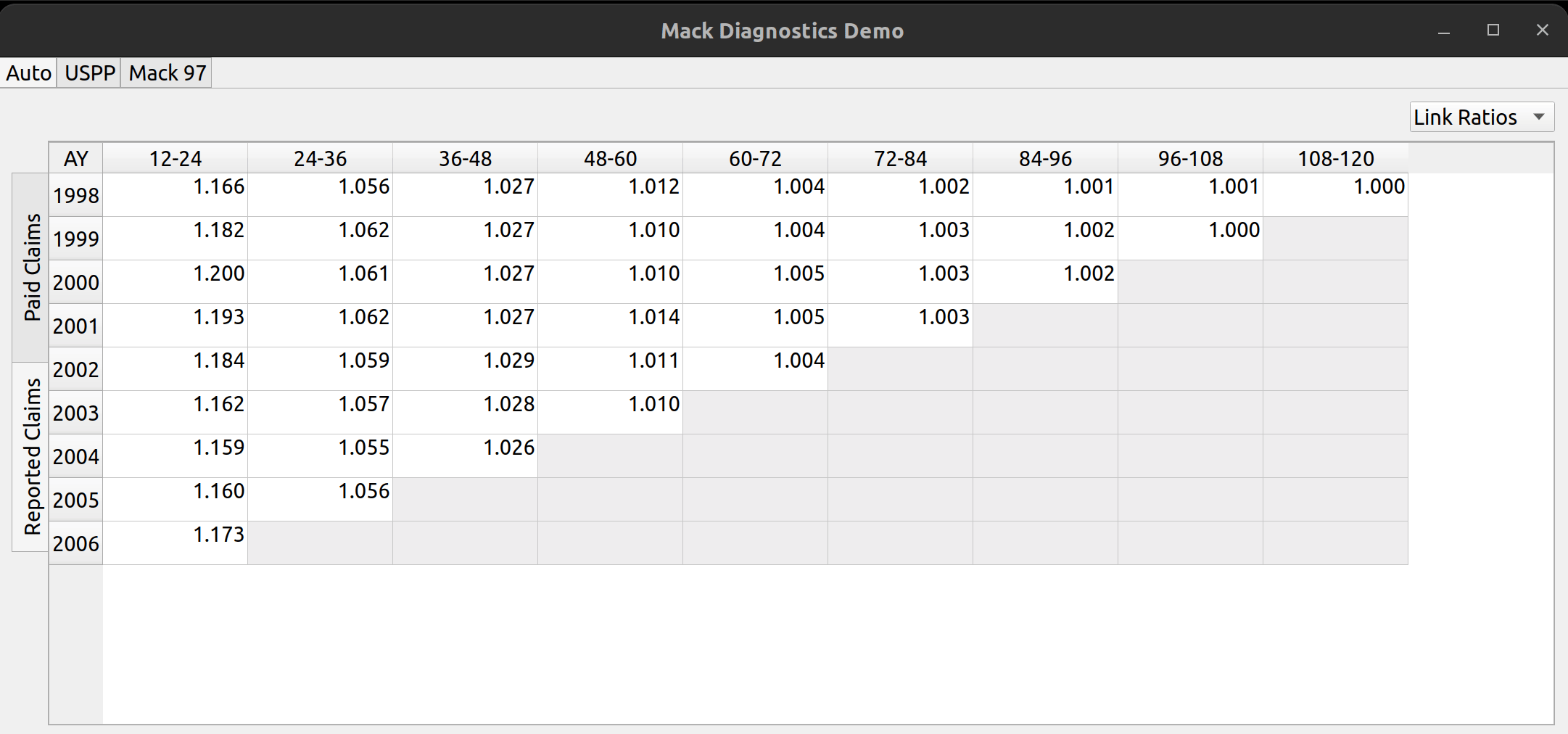
The analysis pane is a widget that allows users to view triangle data for multiple lines of business, and within each line of business, to view multiple types of loss statistics, such as paid losses, incurred losses, case reserves etc. Furthermore, the user may choose to toggle between the values themselves (e.g., actual loss dollar amounts) or link ratios to be used to select loss development factors. Additionally, diagnostic outputs used to test the suitability of each triangle for the chain ladder technique, are included.
The above image illustrates the places on the pane where the user can toggle between these views. At the top left there are three tabs, each of which represents a separate line of business. The image below shows how you can click on each tab to view the data contained in each LOB:
To the left, the user can click on the vertically-rotated tabs to switch between different types of triangle data, such as reported and paid claims:
And, by using the combo box to the right, the user can toggle between raw triangle data and derived link ratios:
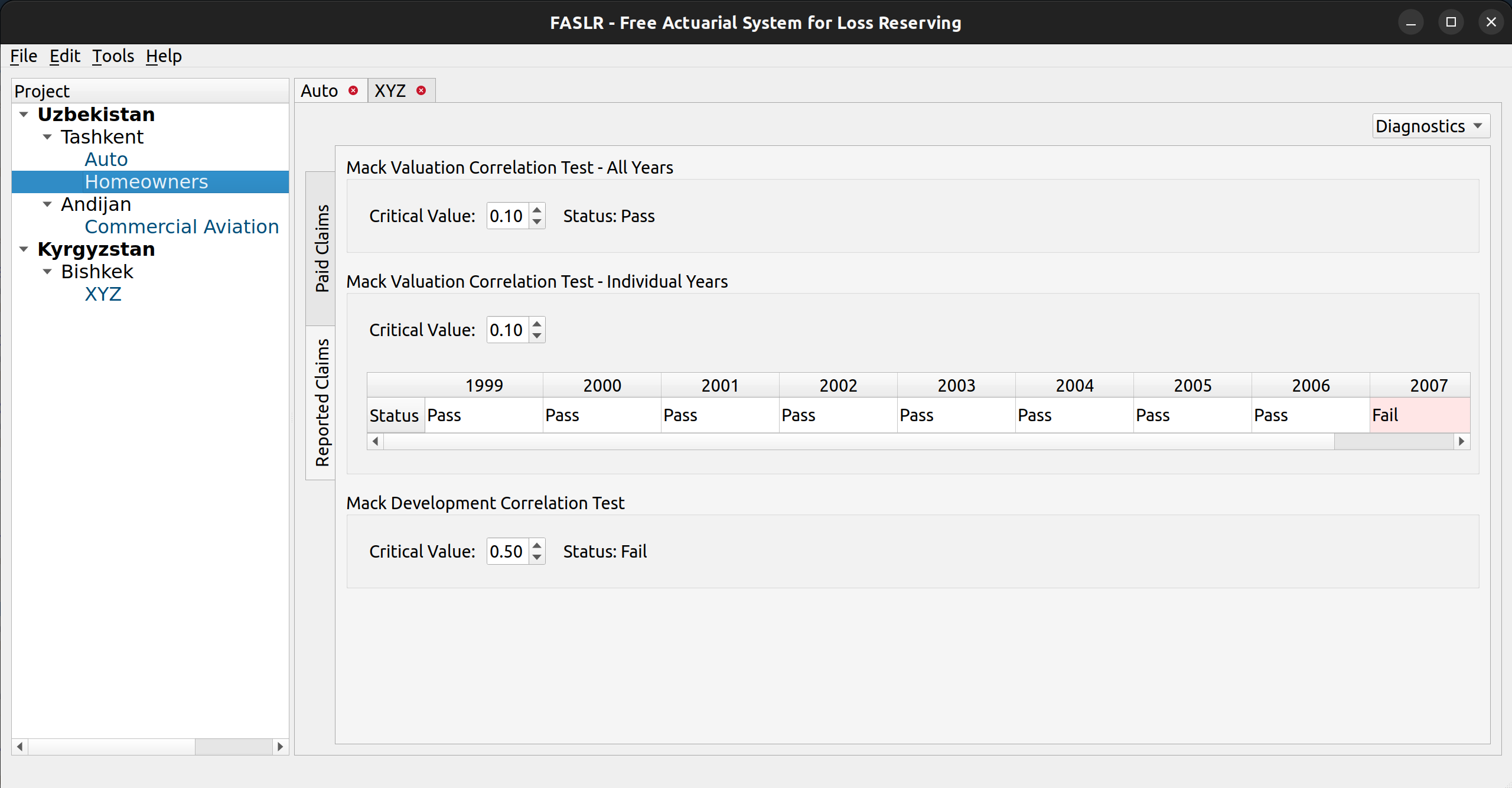
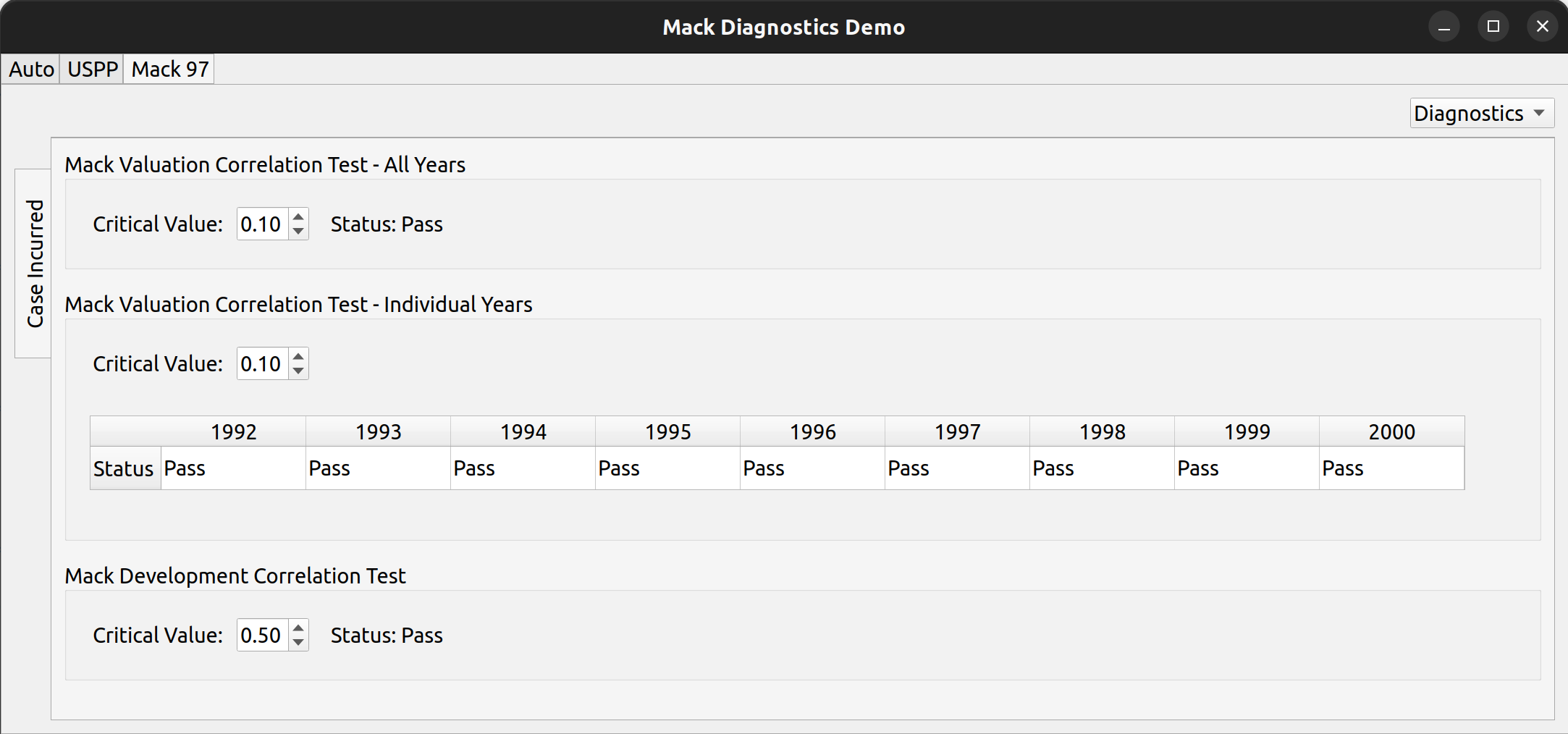
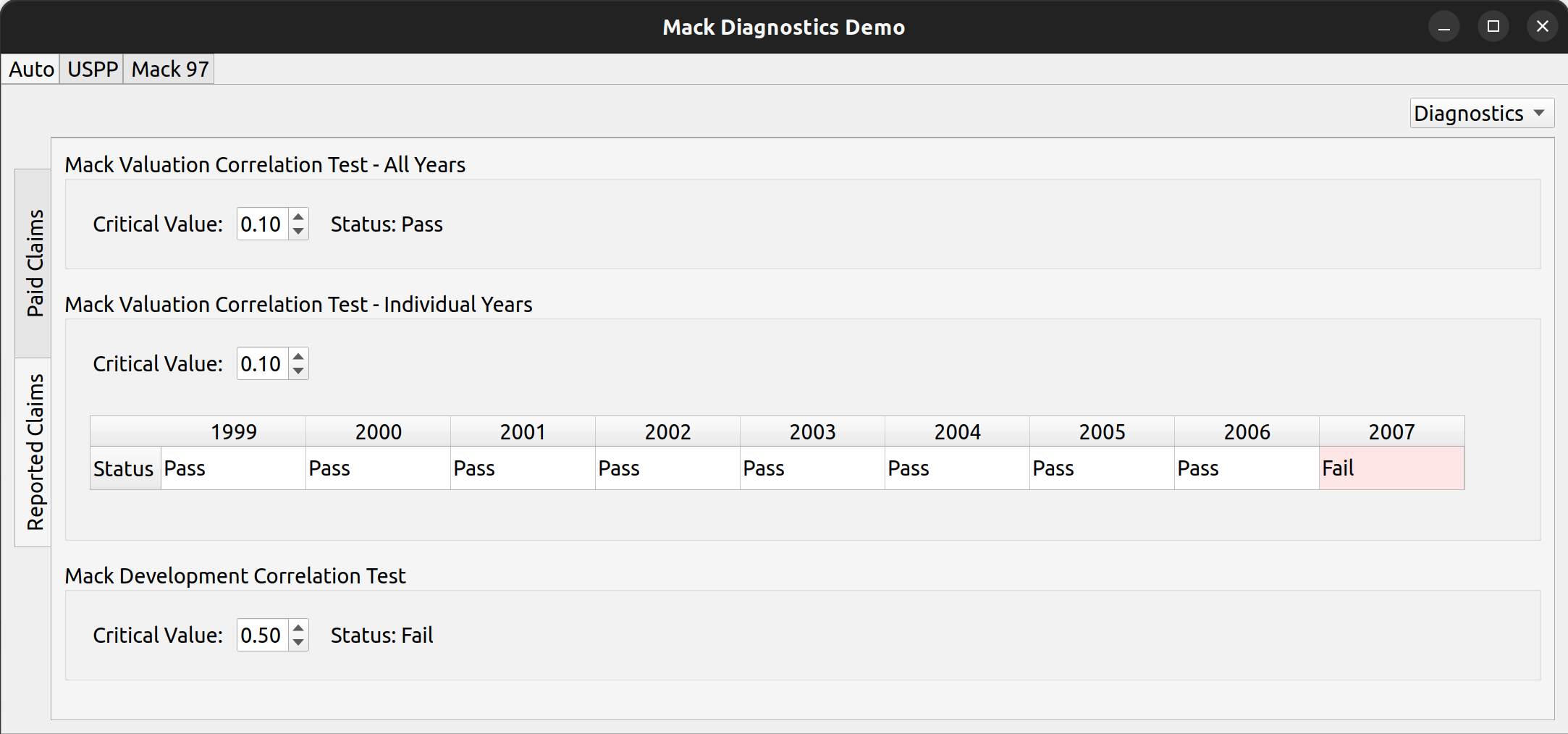
And lastly, the combo box can also be used to view diagnostic tests, the main subject of this post.
Mack Diagnostic Tests
In his 1997 paper, Measuring the Variability of Chain Ladder Reserve Estimates, Thomas Mack describes a set of assumptions underlying the chain ladder technique:
- Successive development factors are not correlated
- Accident years are independent
He then describes a set of diagnostic tests which can be used to validate these assumptions. The first one is called the development correlation test, which compares the magnitude of link ratios for each development period and then uses Spearman’s rank correlation coefficient to test for the correlation between development periods.
This test is available in the chainladder package via the DevelopmentCorrelation class. The second assumption is tested by classifying each development period’s link ratios as being either above or below the median, and then comparing the relative counts of these classifications for each diagonal to test for calendar year effects – such as changes in case management philosophy or the introduction of a new claims handling system. Such effects are considered violations of the second assumption.
This test across calendar years can be conducted either in total for all years or for each individual year. The test for calendar year effects is available in the chainladder package via the ValuationCorrelation class. The chainladder documentation contains tutorials on how to use these tests prior to conducting the chain ladder technique.
FASLR includes these three tests as part of the analysis pane:
In the above image, each of three tests is conducted against the triangle found in Mack’s 1997 paper, and are consistent its results (note that the years here go past 1997 – the original paper didn’t have the years so I made them up). Each test is bound by a groupbox, containing a spin box that allows the user to select the critical value used in the hypothesis test. Below is an example where two of the tests have failed, using one of the auto data sets in Friedland’s reserving paper: