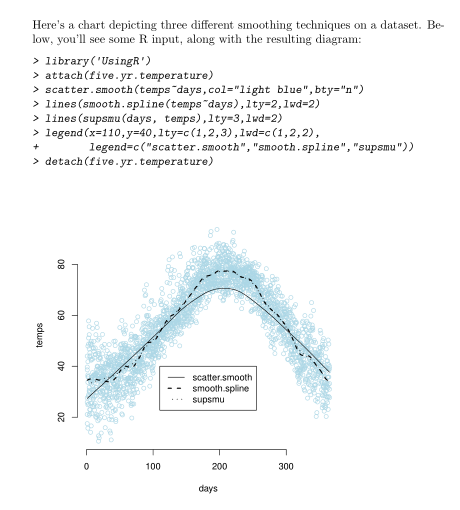
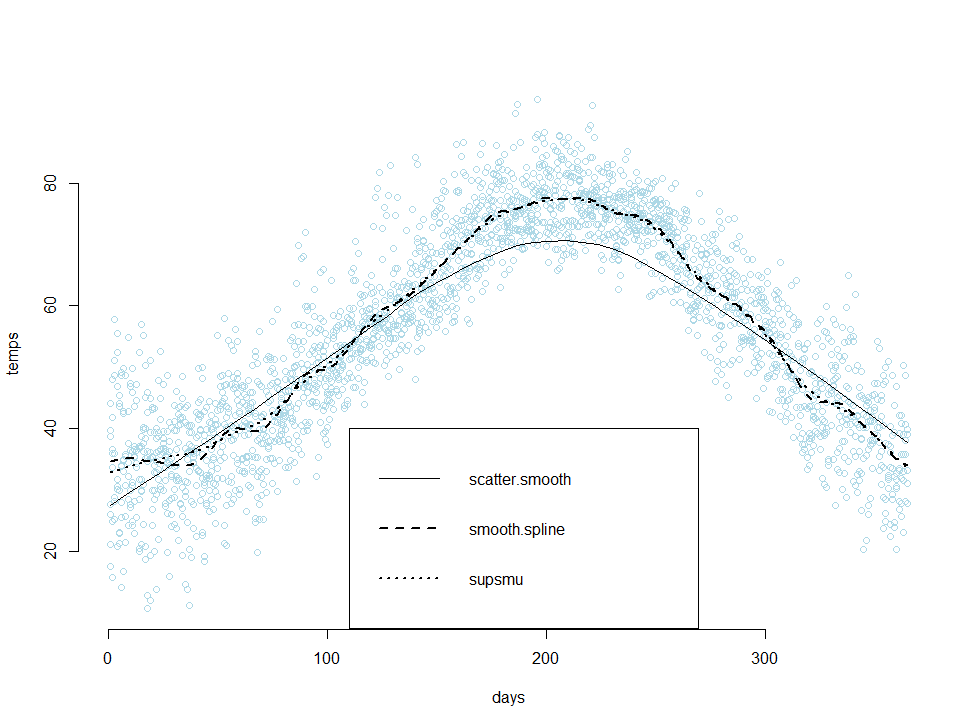
![]() can do some pretty neat things. While it’s mostly known for typesetting mathematical notation, it can also be used to render structural formulas via the chemfig package, which makes it useful in the electronic communication of chemistry concepts – for example, it would allow two chemists located in different countries to chat over a message board, easing collaboration.
can do some pretty neat things. While it’s mostly known for typesetting mathematical notation, it can also be used to render structural formulas via the chemfig package, which makes it useful in the electronic communication of chemistry concepts – for example, it would allow two chemists located in different countries to chat over a message board, easing collaboration.
I’ll demonstrate some of the capabilities of chemfig by rendering the structural formulas of amino acids – 20 distinct molecules that serve as the building blocks of proteins – that is, the basis of cellular activity. Below are structural formulas for 9 of these, the ones with nonpolar side chains (this means that the side chains are hydrophobic, and do not have an affinity for water).
Amino Acid Structure
The basic structure of an amino acid consists of an asymmetric carbon bonded to four components – a hydrogen atom, an amino group, a carboxyl group, and an R-group. The amino group can act as a base, accepting a hydrogen ion. The carboxyl group can act as an acid (hence the name, amino acid), donating a hydrogen ion. The R-group is what gives a particular amino acid its identity (that is, whether a particular amino acid is glycine, tryptophan, etc.). It is unique for each type of amino acid and dictates its behavior. The amino group of one amino acid can bond with the carboxyl group of another amino acid, forming a peptide bond. When several amino acids are linked in a chain, they form a polypeptide – and one or more polypeptides together form a protein molecule.
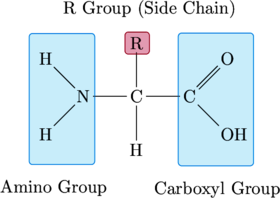
This basic structure serves as a template for each of the amino acids below. The amino and carboxyl groups, together with the asymetric carbon and lower hydrogen atom, form the amino acid’s contribution to the polypeptide backbone. These are highlighted in blue. The R-group, distinct for each amino acid, is highlighted in red.
Notice that each of the code samples below contains a repeating pattern – \chemfig renders the structural formula of the amino acid. \chemmove draws the boxes that highlight the backbone and R-groups.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
\chemfig{ C(-[:180]@{AR}N(-[:135]H)(-[:225]@{AL}H))(-[:0]@{CL}C(=[:45]@{CR}O)(-[:315]OH))(-[:90]@{R}R)(-[:270]H) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-3pt,yshift=-3pt]R.south west) rectangle ([xshift=4pt,yshift=3pt]R.north east) node[xshift=0pt,yshift=5pt,above,opacity=1,orientation]{R Group (Side Chain)}; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-6pt,yshift=-15pt]AL.south west) node[xshift=15pt,yshift=-6pt,below,opacity=1,orientation]{Amino Group} rectangle ([xshift=3pt,yshift=35pt]AR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-3pt,yshift=-39pt]CL.south west) node[xshift=24pt,yshift=-6pt,below,opacity=1,orientation]{Carboxyl Group} rectangle ([xshift=12pt,yshift=12pt]CR.north east) ; } |
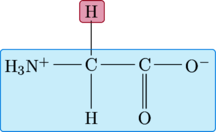
Glycine
For glycine, the R-group is a single hydrogen atom.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]@{R}H) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-3pt,yshift=-3pt]R.south west) rectangle ([xshift=4pt,yshift=3pt]R.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
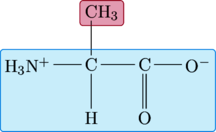
Alanine
The R-group for alanine is a little more complex than that of glycine, consisting of a methyl group instead of a hydrogen atom.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]@{RL}CH_{3}) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-3pt,yshift=-5pt]RL.south west) rectangle ([xshift=16pt,yshift=3pt]RL.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
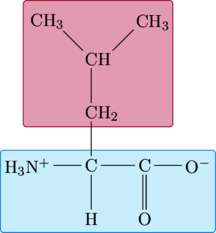
Valine

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]CH(-[:135]CH_{3})(-[:45]@{RR}CH_{3})(-[:180,1,,,draw=none]@{RL})) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-9pt,yshift=-9pt]RL.south west) rectangle ([xshift=15pt,yshift=6pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
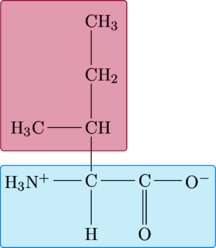
Leucine
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]CH_{2}((-[:90]CH(-[:135]CH_{3})(-[:45]@{RR}CH_{3})))(-[:180,1,,,draw=none]@{RL})) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-9pt,yshift=-9pt]RL.south west) rectangle ([xshift=15pt,yshift=9pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
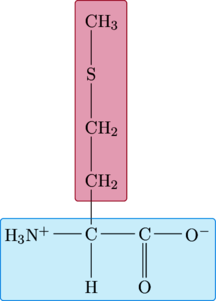
Isoleucine
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]CH(-[:180]@{RL}H_3C)(-[:90]CH_{2}(-[:90]@{RR}CH_{3}))) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-6pt,yshift=-9pt]RL.south west) rectangle ([xshift=18pt,yshift=9pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
Methionine
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]@{RL}CH_{2}(-[:90]CH_{2}(-[:90]S(-[:90]@{RR}CH_{3})))) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-6pt,yshift=-9pt]RL.south west) rectangle ([xshift=18pt,yshift=9pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
Phenylalanine
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]@{RL}CH_{2}(-[:90]*6(-=-@{RR}=-=))) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-33pt,yshift=-9pt]RL.south west) rectangle ([xshift=36pt,yshift=6pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |
Tryptophan
This was definitely the hardest of the amino acids to draw so far. It took multiple attempts to get the ring structure correct. I also had a problem rendering the full image (the top was being cropped off). I actually have an invisible structure embedded in the page code that serves as a workaround to getting the full image rendered.

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})) (-[:90]@{RL}CH_{2}(-[:90]?(*6([::-30]=-NH-(*6(--@{RR}----))=?)))) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-33pt,yshift=-9pt]RL.south west) rectangle ([xshift=36pt,yshift=6pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } \chemfig{ -[:90,1,,,draw=none](-[:90,1,,,draw=none]) } |
Proline
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
\chemfig{ C(-[:0]C(-[:0]@{C}O^{-})(=[:270]O)) (-[:270]H)(-[:180]H_3N^{+}(-[:270,1,,,draw=none]@{A})(-[:90]@{RL}H_{2}C?)) (-[:90]CH_{2}(-[:120]@{RR}CH_{2}?)) } \chemmove{ \draw[ fill=purple, draw=purple, fill opacity=.2, rounded corners=2pt ] ([xshift=-3pt,yshift=-9pt]RL.south west) rectangle ([xshift=42pt,yshift=9pt]RR.north east) ; } \chemmove{ \draw[ fill=cyan, draw=cyan, fill opacity=.1, rounded corners=2pt ] ([xshift=-9pt,yshift=-7pt]A.south west) rectangle ([xshift=3pt,yshift=5pt]C.north east) ; } |