So I’ve finally decided to commit to learning linear algebra, and I think this 70-day series of articles will be just what I need to keep myself motivated throughout the process.
On Spaced Repetition
I took a first course on linear algebra during a five-week period my freshman year of college as part of a frantic rush to finish up my economics degree within 2 years. Although ultimately successful, in hindsight this was a bad idea as I immediately forgot the majority of the material within a matter of weeks – covering an entire course within such a short period of time with no reinforcement afterwards led to a failure in committing the material to long-term memory. This would lead to problems later on college as so much of the coursework in applied mathematics, statistics, and economics required the student to have a firm footing in linear algebra.
I didn’t realize it at the time, but during my late high school and early college years I employed a crude method of what is known as spaced repetition, a learning technique geared towards the long-term retention of material. For a given course, my typical study schedule was as follows:
Day 1 – Chapter 1
Day 2 – Chapter 2
Day 3 – Chapter 3
Day 4 – Chapter 4
Day 5 – Chapter 5
Day 6 – Chapters 1 & 6
Day 7 – Chapters 2 & 7
Day 8 – Chapters 3 & 8
Day 9 – Chapters 4 & 9
Day 10 – Chapters 5 & 10
…and so on. This method led to good results for year-end finals and end-of semester exams, but now that it has been several years I find myself struggling to recall the dates of important civil war battles or the names of major dynasties in imperial China. And that’s really a shame since it doesn’t take much more than two repetitions of the material to really make something stick. So two main failures of my study technique were inefficiency and long-term retention. Inefficiency in the sense that I didn’t know how to properly space revisits to the material and failure in long-term retention in the sense that I didn’t revisit the material after the course was over.
Implementation
For more information on spaced-repetition, I suggest reading an excellent article by gwern to understand how it works and what techniques people have used to implement it. The question is now that I have come across this wonderful idea on how to retain information over years, how can I effectively apply these techniques in a practical sense? One of my friends Riley in the actuarial community showed me a physical method for studying life contingencies formulas:
By the time I saw this, I had already been using software, so I found this method hilarious in the sense that this method is impractical once you have a large number of cards, say over 1000, but also ingenious in that someone has managed to apply the technique without the use of a computer.
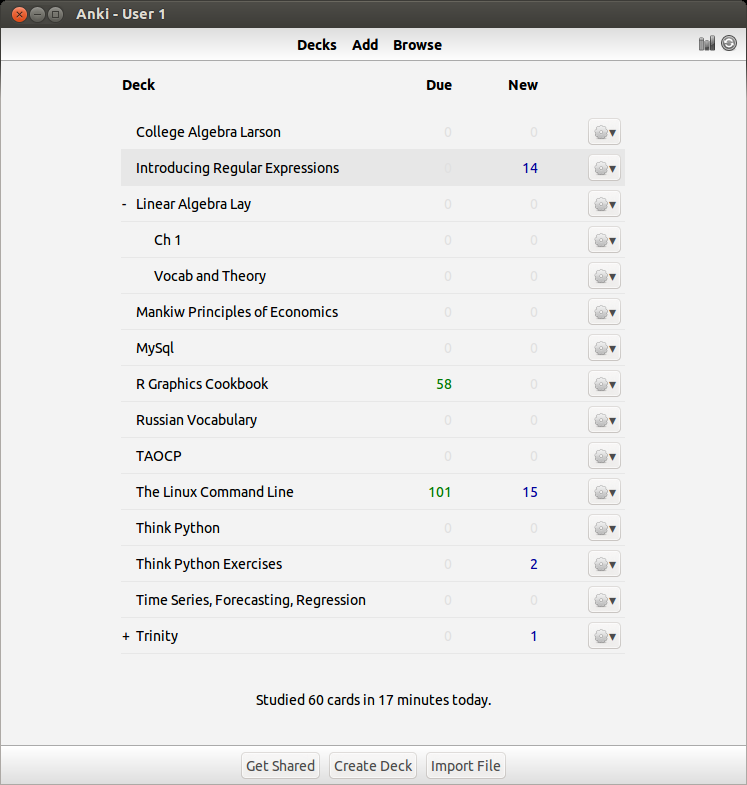
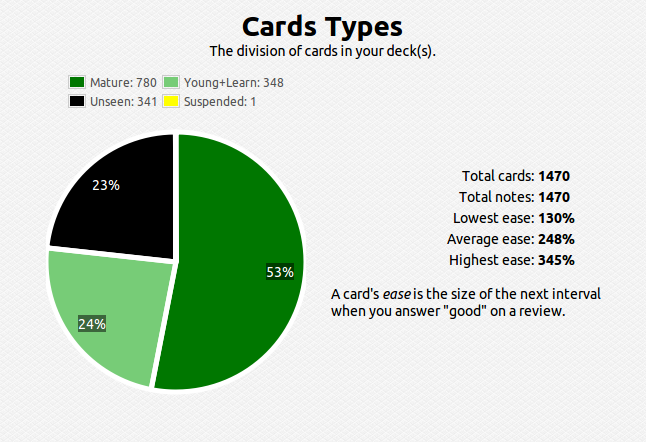
Like I said, once the number of facts becomes large, figuring out the optimal spacing between revisits of material becomes cumbersome and practically impossible to track – this problem also becomes apparent when the gap between revisits becomes large, say, over a year. To solve this problem I use a software called anki, which digitally stores your cards and calculates the time between reviews automatically. Here’s what my current deck looks like so far over the short and long run:
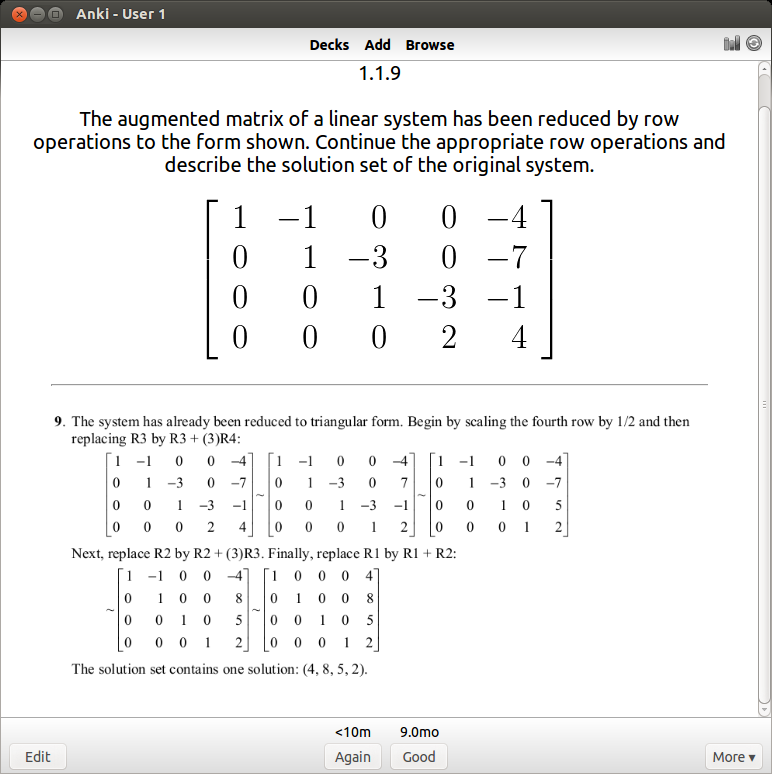
You can see that I have about 1400 cards covering various subjects. This technique is extremely efficient – you review the material that you are struggling with multiple times and the material you’ve mastered less often. For example, a typical review card would look like this:
If I get it right, I won’t see the card again for another 9 months. I’ve actually done this problem several times, so 9 months is an indication that I know it well. If I get it wrong, I have to review it again and the review gap goes back down to zero days. For newer cards, the time until next review will be shorter (4 days).
So, it has taken me quite some time to get to this point – the idea that you can use computers to efficiently commit mathematics to long term memory is incredible. I feel so fortunate to have these tools available to me today. Some technical skills are involved, in particular you need to know LaTeX to get the mathematical notation onto the cards. That itself took a while to learn, but I’m glad I’m finally at the point where I can apply this learning method to mathematics.
There are almost 2,000 problems and 70 sections in David Lay’s linear algebra book, hence, 70 days of linear algebra. I plan to complete all 70 sections problems within 70 days, but that doesn’t mean I will stop doing problems after 70 days, that is just for a first run through the material. Creating a deck of anki cards is actually a very time consuming process, and in that respect I imagine myself only being able to create cards for 2 sections per week. But given that the point of the project is to be able to retain the information over the course of a lifetime, I believe the investment is worth it (I figure if people can use anki to memorize all of Paradise Lost, 2000 problems should be a piece of cake).



Pingback: No. 109: Interlude | Gene Dan's Blog
Awesome post! Did you use a textbook? Are you open to sharing your deck?